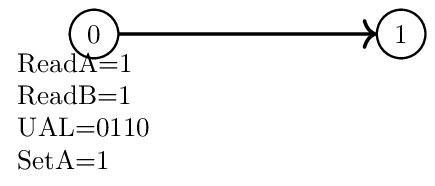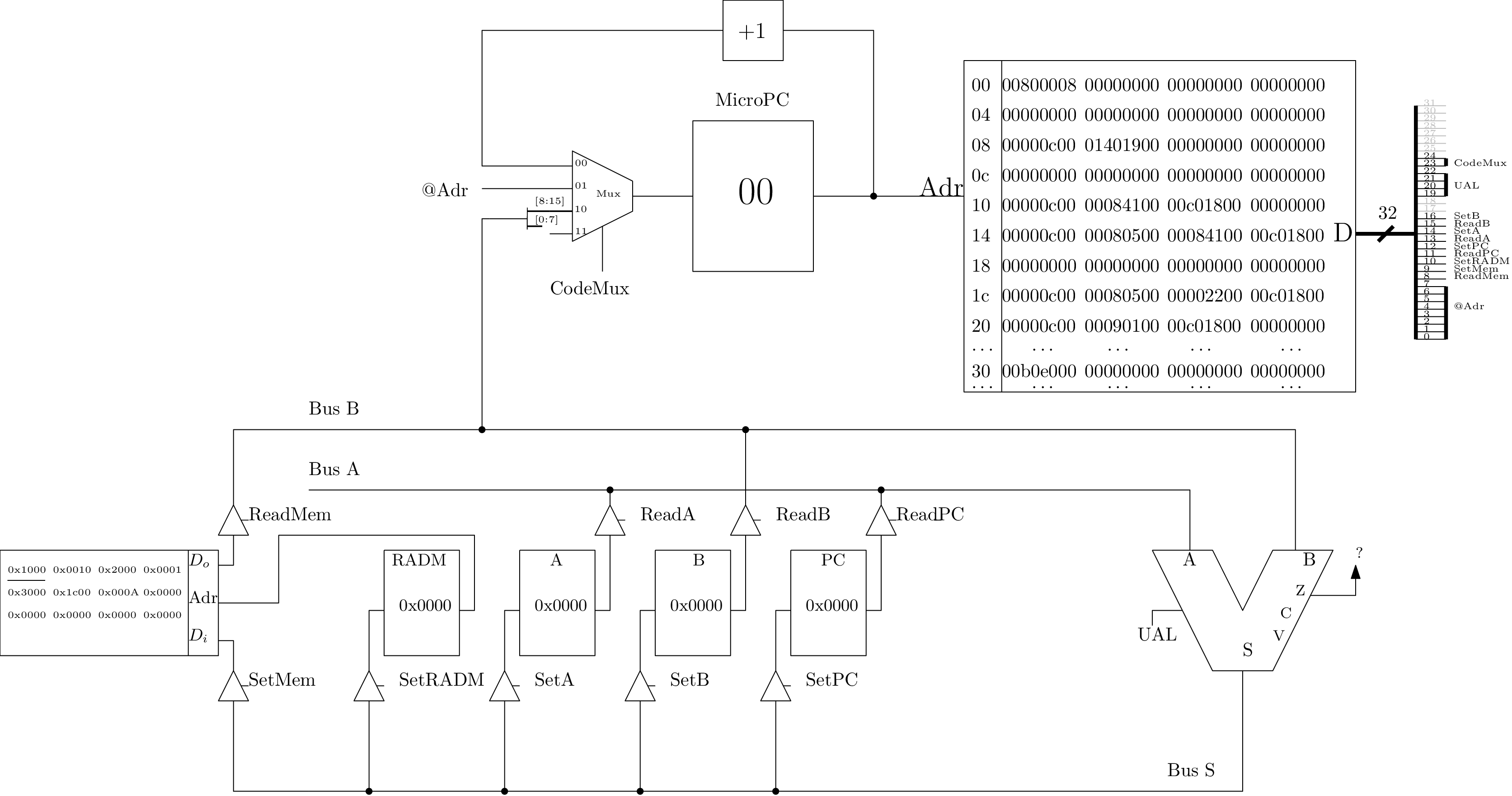Architecture des ordinateurs

Réalisation électronique d’une machine programmable manipulant des représentations numériques

Jérémy Fix

CentraleSupélec

2025-11-02

Architecture des ordinateurs

Architecture des ordinateurs

ou plutôt

Réalisation électronique d’une machine programmable manipulant des représentations numériques

Philosophie et programme du cours

Philosophie du cours

Introduire les concepts sous-jacents à n’importe quelle architecture sans être un cours sur une architecture spécifique (ARM, Intel, MIPS, ..)

Abstraction progressive allant du bit à une architecture exécutant un jeu vidéo

Au programme

• 4 CM (1h30) ⇒ représentations numériques, électronique, premier chemin de données, séquenceur
• 2 TPs (4h) : séquenceur manuel et micro-programmé
• 2 CM (1h30) ⇒ pile et programmation
• 1 TP (4h) : Programmation
• 1 x 1h30 ⇒ mémoires, périphériques et interruptions
• 2 TPs (4h) : périphériques, interruptions, ordonnanceur et place aux jeux

Intervention STMicro (Sébastien Ferroussat) 3h30: Architectures ARM

Site web : https://jeremyfix.github.io/Architecture/

Evaluation

Examen écrit 2h

Contenu technique

On va introduire :

• le codage binaire,
• les transistors,
• les systèmes logiques,
• la programmation,
• les périphériques, interruptions

Démonstration

Space Invaders (1978)

Codage et opérations binaires

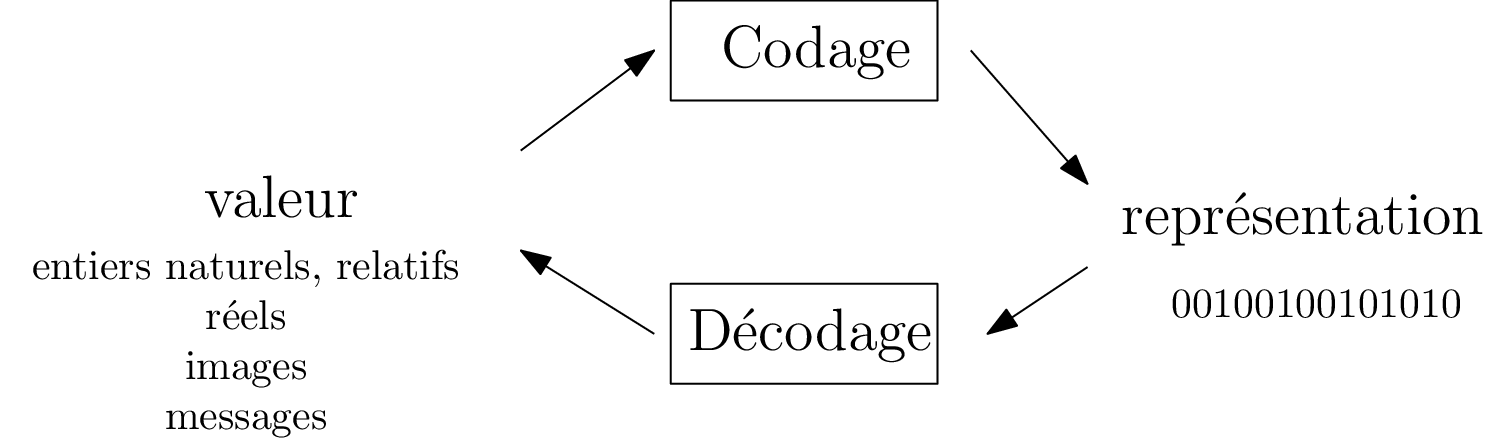
Représenté et représentant

Une valeur, quelle que soit sa nature, doit être représentée en binaire :

Bonne représentation ?

• facile à coder/décoder/manipuler, avec ou sans pertes
• robuste aux perturbations, compact

Représentation des entiers naturels - Histoire

Systèmes additif des Egyptiens, un symbole par puissance de 10

Système mixte additif/postionnel des Mésopotamiens

Système positionnel Shadock

Figure 1: Systèmes de numération

• Système Egyptien, un symbole par puissance de 10: \(1527\)

• Système Mésopotamiens en base 60 :

\(1527 = (20 + 5) \times 60^1 + (20 + 7) \times 60^0\)

• Système Shadoks Bu-Zo-Ga-Mu

\(99 = 1 \times 4^3 + 2 \times 4^2 + 0 \times 4^1 + 3 \times 4^0\)

Système positionnel

En base 10 : \[34 = 3 \times 10^1 + 4 \times 10^0\]

En base p : \[(a_{k-1}a_{k-2}\cdots a_{1}a_{0})_p = \sum_{i=0}^{k-1} a_i p^i\]

avec \(\forall i, a_i \in [0, p-1], a_{k-1} \neq 0\)

Conversion de base

Comment passer de la représentation base p à la valeur en base 10 ? \[(a_{k-1}a_{k-2}\cdots a_{1}a_{0})_p = \sum_{i=0}^{k-1} a_i p^i\]

Comment passer de la valeur \(n\) en base 10 à la représentation en base p ? \[\sum_{i=0}^{k-1} a_i p^i = a_0 + p \times (\sum_{0}^{k-2} a_{i+1} p^i)\]

⇒ division euclidienne par \(p\)

Représentation binaire : \(39 = 100111_2\)

\[\sum_{i=0}^{k-1} a_i p^i = a_0 + p \times (\sum_{0}^{k-2} a_{i+1} p^i)\]

Méthode des divisions successives :

Division	Quotient	Reste
39 ÷ 2	19	1
19 ÷ 2	9	1
9 ÷ 2	4	1
4 ÷ 2	2	0
2 ÷ 2	1	0
1 ÷ 2	0	1

Vérification :

Puissance de 2	\(2^5 = 32\)	\(2^4 = 16\)	\(2^3= 8\)	\(2^2=4\)	\(2^1 = 2\)	\(2^0 = 1\)
\(39_{10}\)	1	0	0	1	1	1

• \((a_{k-1}a_{k-2}\cdots a_1 a_0\) est un mot, dont \(a_{k-1}\) est le bit de poids fort et \(a_0\) le bit de poids faible

Représentation hexadécimale : \(39 = 27_{16}\)

16 chiffres : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Division par 16 :

Division	Quotient	Reste
39 ÷ 16	2	7
2 ÷ 16	0	2

Ou, à partir de la représentation binaire : \[39_{10} = (\overbrace{0010}^{2}\quad\overbrace{0111}^{7})\]

Autres exemples :

• \(176_{10} = B0_{16}\)
• \(255_{10} = FF_{16} = 15 \times 16^1 + 15\)

Autres systèmes de codage

Décimal codé binaire (BCD - Binary Coded Decimal)

\[421 = \overbrace{0100}^{4} \overbrace{0010}^{2} \overbrace{0001}^{1}\]

Code de Gray

valeur	représentation binaire	représentation de Gray
0	000	000
1	001	001
2	010	011
3	011	010
4	100	110
5	101	111
6	110	101
7	111	100

Addition binaire

Exemple : 001 + 011

Demi-additionneur : \[(a,b) \rightarrow (retenue, reste)\]

\(a\)	\(b\)		Retenue	Reste
0	0		0	0
0	1		0	1
1	0		0	1
1	1		1	0

Additionneur complet : \[(a, b, r) \rightarrow (retenue, reste)\]

\(a\)	\(b\)	\(r\)	Retenue	Reste
0	0	0	0	0
0	1	0	0	1
1	0	0	0	1
1	1	0	1	0
0	0	1	0	1
0	1	1	1	0
1	0	1	1	0
1	1	1	1	1

• Algorithme d’addition de représentations non signées
• Précision finie ⇒ \(n \in [0, 2^{k}-1]\) et bit de carry

Autres opérations arithmétiques

Soustraction :

• a - b , a ≥ b
• posée avec emprunt de retenue (e.g. \(105_{10} - 16_{10}\), \(100_2 - 001_2\))

Multiplication :

• addition et décalage (e.g. \(39_{10} \times 5_{10}\))

Division :

• posée (e.g. \(39_{10} / 5_{10}\))

Entiers négatifs ?!

Représentation des entiers relatifs

Codage par décalage (excess-K)

• \(n \in [-2^{k-1}, 2^{k-1}-1]\), \(K = 2^{k-1}\)
• Codage : \(x = EncUB_k(n + K)\), \(n+K \in [0, 2^k -1]\)
• Décodage : \(n = DecUB(x) - K = \sum_{i=0}^{k-1} x_i 2^i - 2^{k-1}\)

\(n\)	-4	-3	-2	-1	0	1	2	3
\(x\)	\(000_{2K}\)	\(001_{2K}\)	\(010_{2K}\)	\(011_{2K}\)	\(100_{2K}\)	\(101_{2K}\)	\(110_{2K}\)	\(111_{2K}\)

• addition particulière (\(-4 +_{UB} 1 \neq -3\), k=3)
• comparaison facile.

Codage par valeur signée (sign-magnitude)

• \(n \in [-2^{k-1}+1, 2^{k-1}-1]\)
• un bit de signe, k-1 bits de valeur

\(n\)	-3	-2	-1	0	1	2	3
\(x\)	\(111_{2s}\)	\(110_{2s}\)	\(101_{2s}\)	\(100_{2s}\) ou \(000_{2s}\)	\(001_{2s}\)	\(010_{2s}\)	\(011_{2s}\)

• \(2\) représentations de \(0\),
• Addition particulière(\(1 +_{UB} (-1) \neq 0\), k=3).

Codage par complément à deux (2’s complement)

• Soit \(a=(a_{k-1}a_k\cdots a_0)_2\), trouver \(b=(b_{k-1}b_k\cdots b_0)_2\) tel que

\[a +_{UB} b = 0 \Rightarrow b = \bar{a} + 1\]

car \(\bar{a} + a = 11\cdots 1\)

• On note \(\bar{a} = a_{1C}\) le complément à \(1\), \(a_{2C} = a_{1C} + 1\) le complément à \(2\)

• \(n \in [-2^{k-1}, 2^{k-1}-1]\)

\(n\)	-4	-3	-2	-1	0	1	2	3
1C	(011)	100	101	110	111 ou 000	001	010	011
2C	100	101	110	111	000	001	010	011

• les opérations sont les mêmes, par construction, qu’avec les représentations non signées, e.g. \(2_{10} + (-3)_{10}\)
• comparaison : 1) tester le signe 2) sinon la valeur
• une seule représentation du \(0\)
• débordement (overflow); e.g. k=3 : 3 + 3 ; (-3) + (-3), vérifiable avec les bits de retenue entrante/sortante du bit de poids fort

Représentation des nombres réels - Virgule fixe

Virgule fixe (fixed-point)

• \(26.5 = 2 \times 10^1 + 6 \times 10^0 + 5 \times 10^{-1}\)
• Codage du « . » ? \(26.5 = 11010.1_2\); Convention \(Q<n_e><n_f>\)
• Codage : représentation non signée de \(n \times 2^{n_f}\) sur \(n_e+n_f\) bits,
• Décodage : \(n = \sum_{i=0}^{k-1} a_i 2^{i - n_f} = 2^{-n_f} \sum_{i=0}^{k-1} a_i 2^i\)
• complément à deux (e.g. \(5.25 - 3.5\) ; \(-5.25 + 3.5\) en Q4.2)
• même opérations arithmétiques que pour les entiers (implémentation peu coûteuse sur DSP/FPGA)

Mais :

• précision uniforme,
• non représentation de valeurs particulières (e.g. \(\infty, NaN\), ..)

Virgule flottante IEEE 754-2008

Virgule flottante IEEE 754-2008 (floating-point)

• Introduite dans les années 1980, révisée en 2008 puis 2019,
• Notation scientifique en base p :

\[x = \pm m \times p^{e}, m \in [0, p[, e \in \mathbb{Z}\]

• \(1245 = 1.245 \times 10^3 = 0.1245 \times 10^4 = 0.01245 \times 10^5\)
• représentations dénormalisées (\(e = 0\)); représentation normalisée (\(e \neq 0\))
• En binaire , \(m \in [0, 2[\); Étendu \(\mathbb{R} \cup \{-\infty, \infty\} \cup \{\text{sNan}, \text{qNan}\}\)

signe S (1 bit)	exposant E (\(n_e\) bits)	mantisse M (\(n_m\) bits)

• M code uniquement la partie fractionnaire, premier bit implicite (\(0\) pour les dénormalisées ou \(1\) pour les normalisées).

• E en excess-K (plutôt que complément à \(2\)) permet de comparer deux nombres comme des entiers par comparaison bit à bit en partant des bits de poids fort : le signe à gauche, l’exposant en excess-K puis la mantisse.

• Plusieurs conventions : binary-16, binary-32, binary-64

• Arrondis : \((0.9 / 3) \times 3 \neq 0.9\)

Binary-16

Représentation sur 16 bits, \([-65504, \cdots -2^{-24}, \pm 0, 2^{-24}, \cdots, 65504] \cup \{\pm \infty, NaN\}\)

• 1 bit de signe,
• \(n_e = 5\) bits pour l’exposant, \(K=2^{n_e-1}-1 = 15 = E_{max}\), \(E_{min} = 1 - E_{max} = -14\)
• \(n_m=10\) bits pour la mantisse

Signe	Exposant	Mantisse	Valeur représentée	Note
0	00000	\(0 \cdots 0\)	+0
1	00000	\(0 \cdots 0\)	-0
s	00000	\(0\cdots 01\)	\((-1)^s 2^{-14} (2^{-10}) = (-1)^s 2^{-24}\)	Plus petit dénormalisé
s	00000	\(0\cdots 10\)	\((-1)^s 2^{-14} (2^{-9}) = (-1)^s 2^{-23}\)	Second plus petit
s	00000	\(1\cdots 11\)	\((-1)^s 2^{-14} (\sum_{1}^{n_m} (2^{-i}))=(-1)^s (2^{-14} - 2^{-24})\)	Plus grand dénormalisé
s	00001	\(0\cdots 00\)	\((-1)^s 2^{1-15} = (-1)^s 2^{-14}\)	Plus petit normalisé
s	11110	\(1\cdots 11\)	\((-1)^s 2^{30-15} (1+\sum_{1}^{n_m} 2^{-i}) = (-1)^s (2^{16} - 2^{5})\)	Plus grand normalisé
s	11111	\(0\cdots 00\)	\((-1)^s \infty\)
x	11111	\(\neq 0\)	NaN (sNan ou qNan)	Exception, e.g 0/0, ..

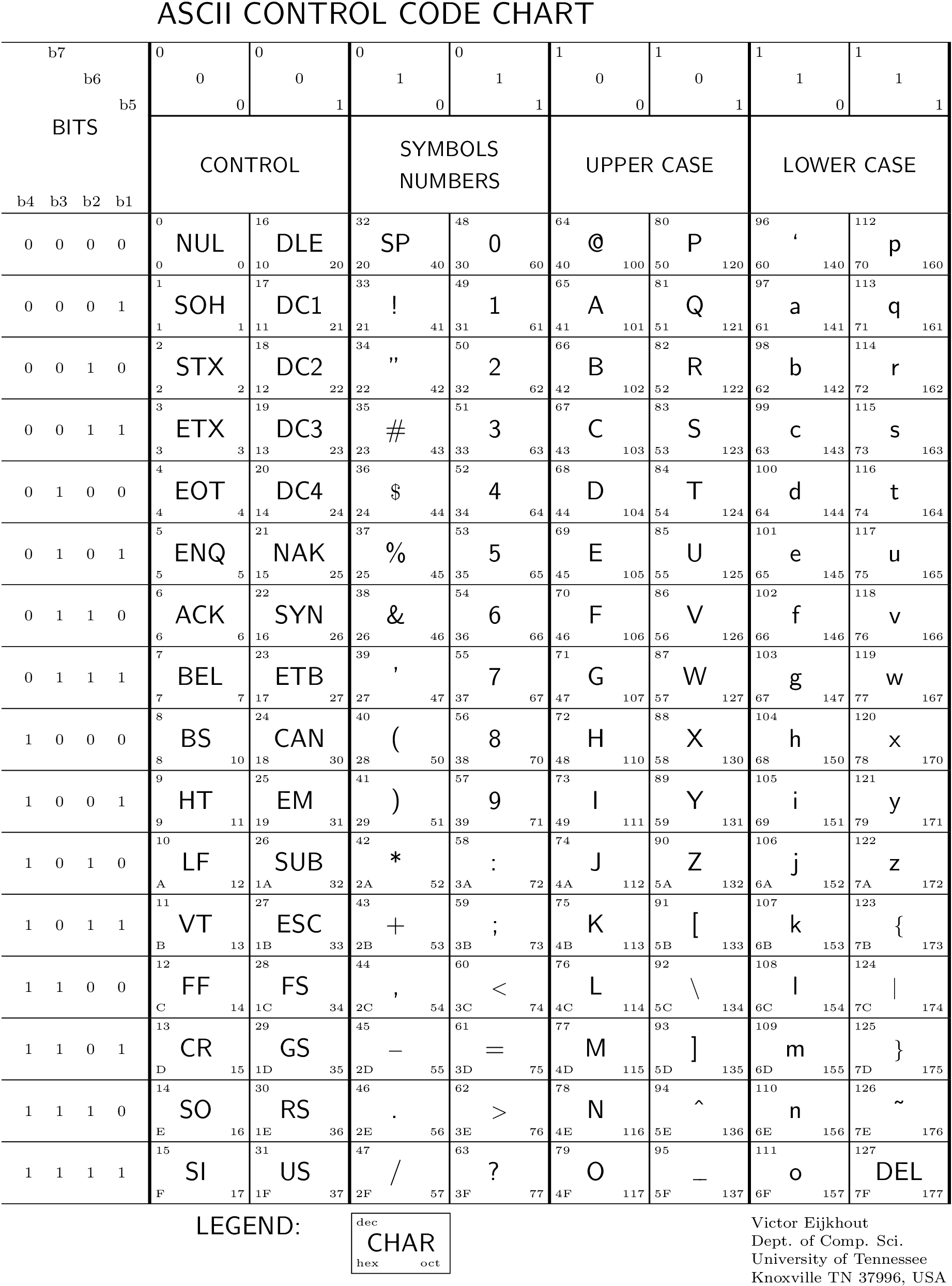
Représentation des caractères

Codage ASCII sur \(7\) bits, \(1960\)

Table ASCII

Caractères “spéciaux” : \t, \n \r, ..

Example en python : la variable \(c\) représente t’elle un caractère ? ord: \(char \mapsto int\), chr: \(int \mapsto char\)

Norme trop spécifique à l’américain \(\rightarrow\) Multiplicité des normes ISO-8859-x sur 8 bits \(\rightarrow\) Norme UTF-8

Devinette

Quelle est la valeur de \((626F6E6A6F757221)_{16}\) ?

• « bonjour! » en ASCII

• 7 093 009 341 547 377 185 , entier non signé sur 64 bits

• 14480052349522733102450775254250229377476974924293223733945531132203847956887992208286226936208445339488307903550918130967917638220682751840913406310573280664198578176 , IEEE binary-64

• , un octet code un niveau de gris (0:noir, 255:blanc)

La couche physique

Représentation physique et manipulation d’un bit

Représentation

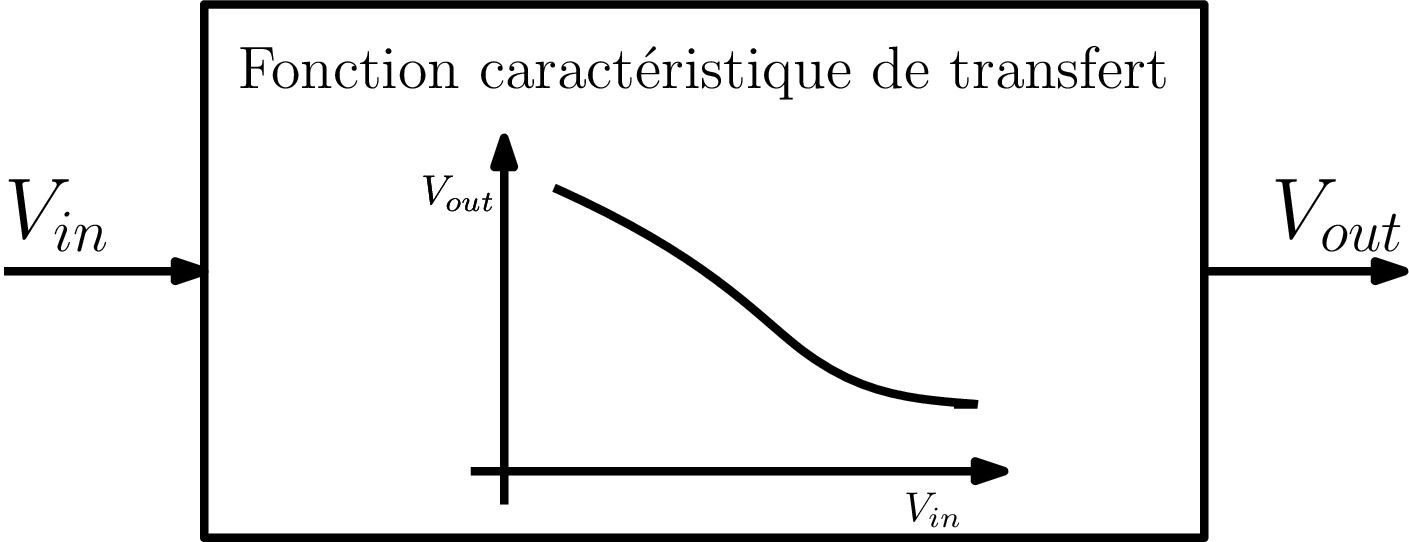
Un bit (0, 1) va être représenté physiquement par un niveau de tension
Par une valeur ? Par des domaines contigus ? Séparés par des marges ?

Manipulation

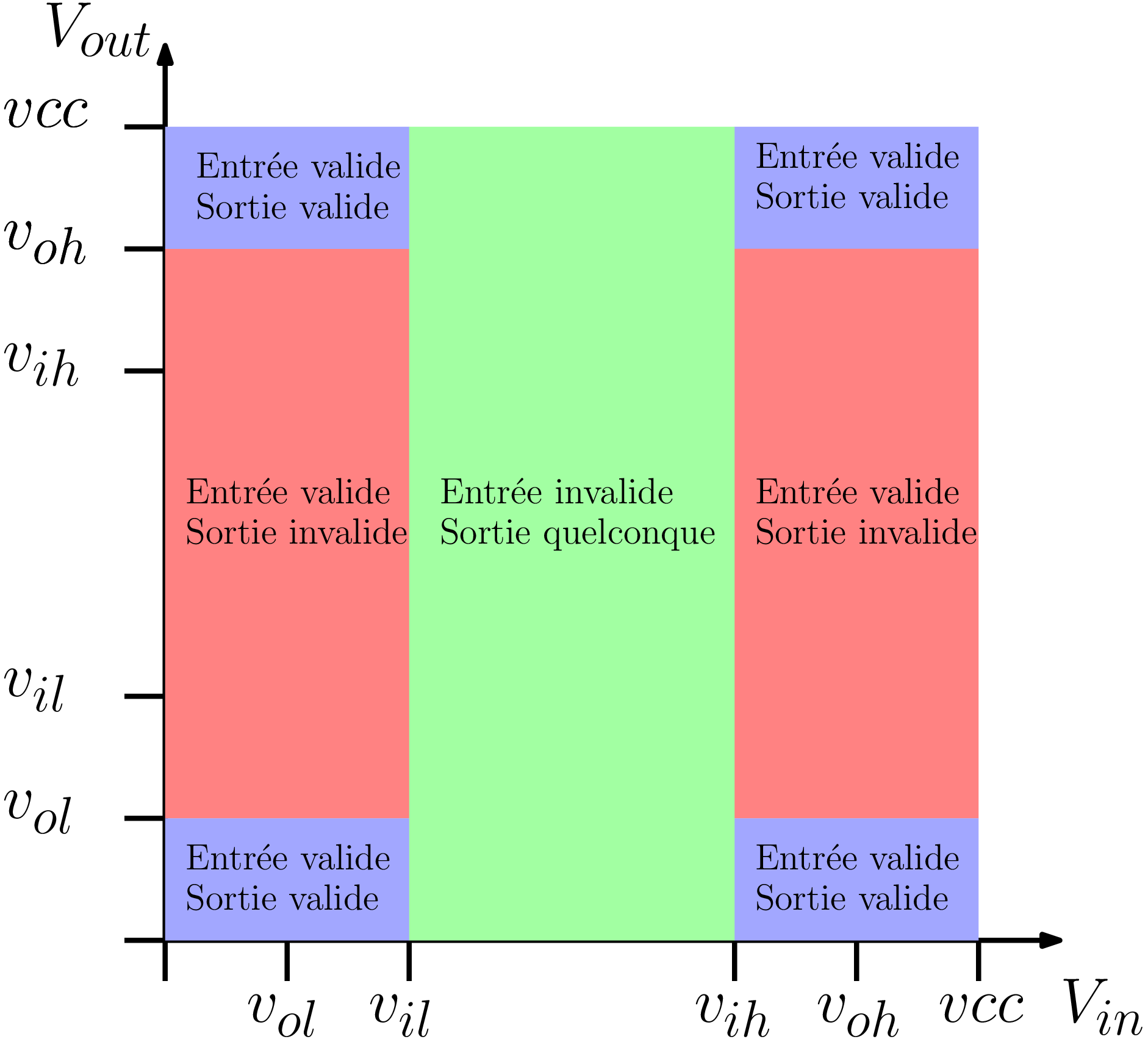
Des marges différentes en entrée et en sortie.

Il nous faut un composant avec une VTC (Votlage Transfer Characteristics) non linéaire

Au début, le relais ou le tube à vide

Relais électromécanique de J. Henry (1930-1940), basculant en quelques millisecondes

Les premiers ordinateurs ENIAC/EDVAC 1946 utilisaient 20K tubes à vides, basculant en quelques microsecondes

Voir First draft report on the EDVAC. J. Von Neumann

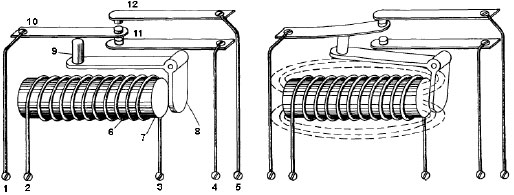
Puis vient le transistor (1947)

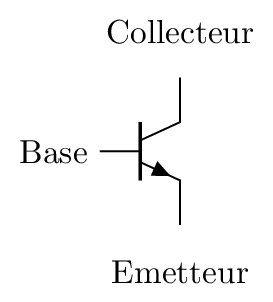
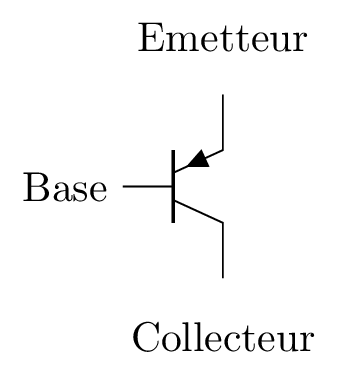
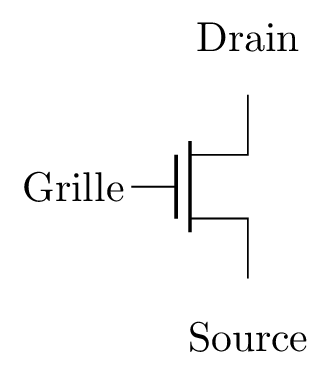
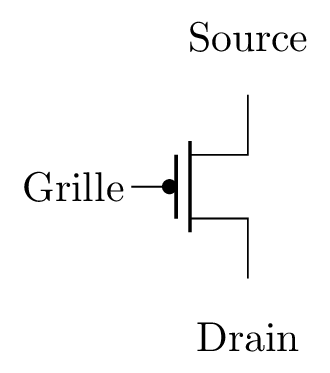
1. Transistor bipolaire NPN TTL. b) Transistor bipilaire PNP TTL. c) Transistor unipolaire NMOS. d) Transistor unipolaire PMOS

Bascule en quelques dizaines de nanosecondes.

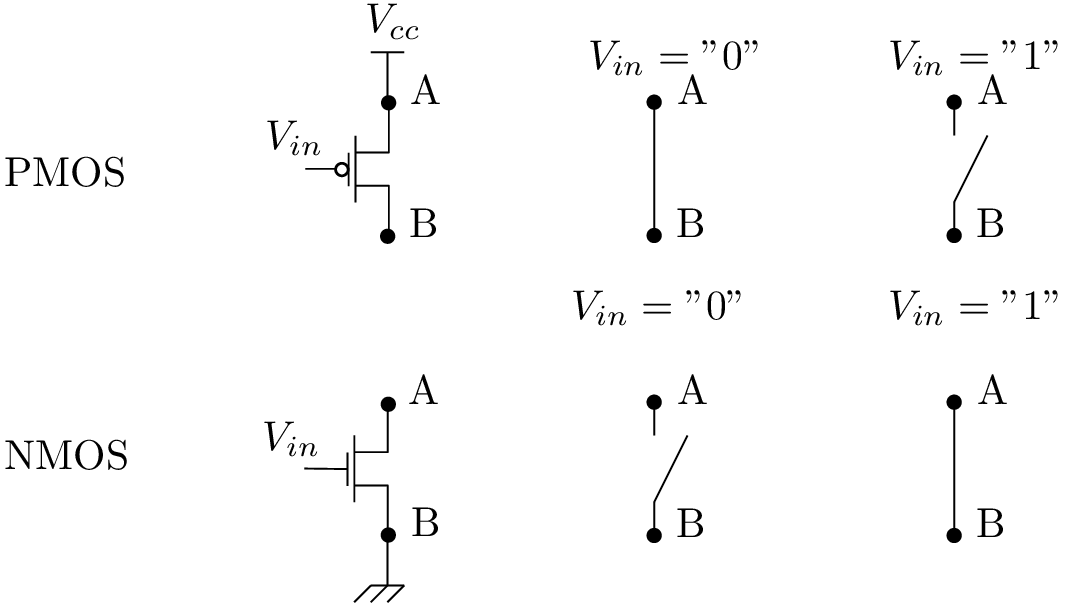
Un interrupteur commandable : CMOS et circuits

1. Caractéristiques des transistors NMOS et PMOS
   
2. Utilisation en interrupteur, en technologie CMOS

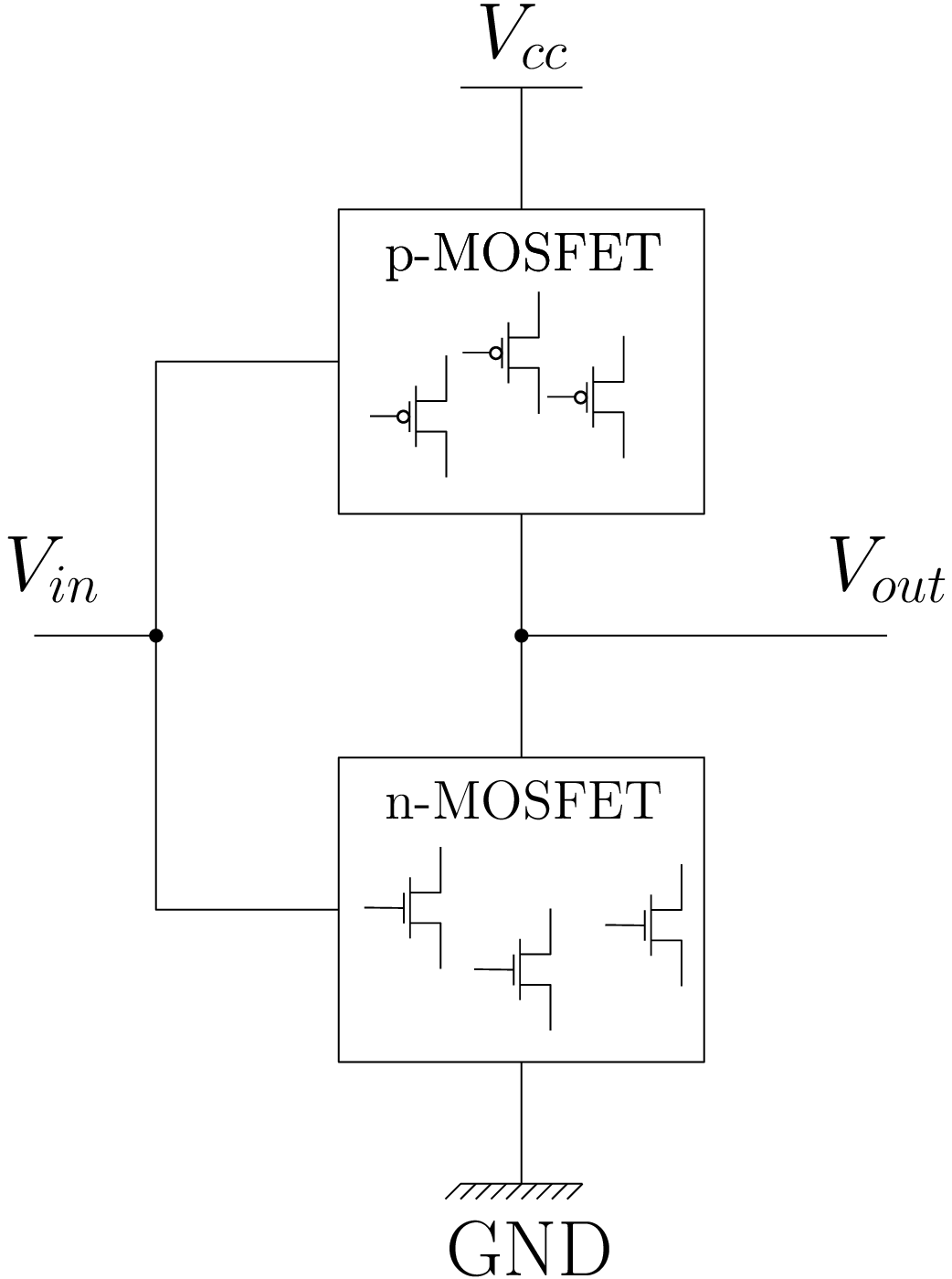
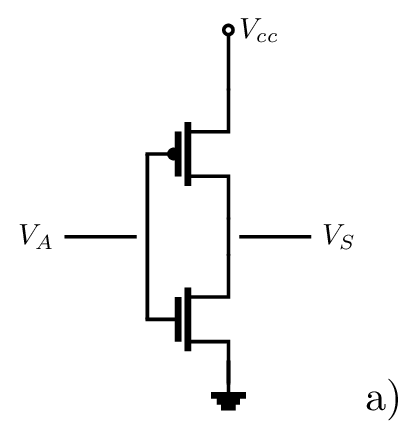
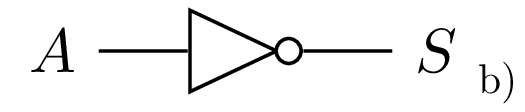
Notre premier circuit : Inverseur (Not) : \(S=\overline{A}\)

1. Une réalisation possible d’une porte NOT en technologie CMOS.
   
2. Symbole normalisé (norme Américaine).

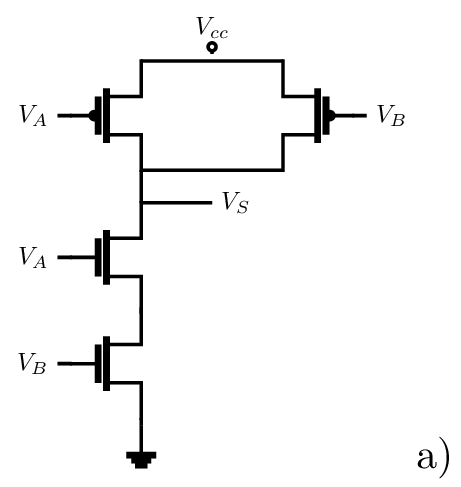
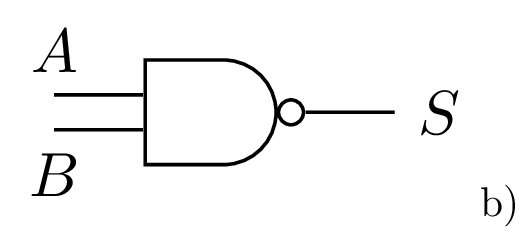
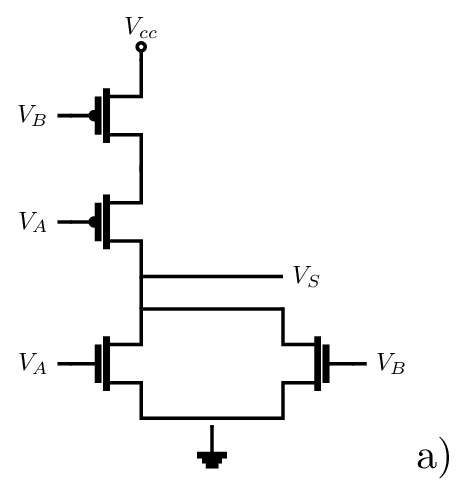
Circuit à deux entrées : Porte NAND : \(S = \overline{A.B}\)

1. Une réalisation possible d’une porte NAND en technologie CMOS.
   
2. Symbole normalisé

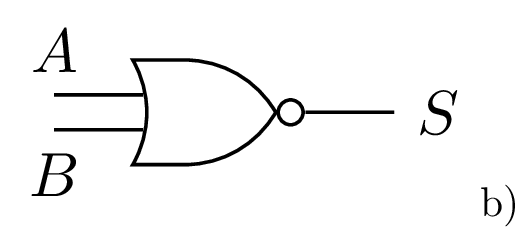
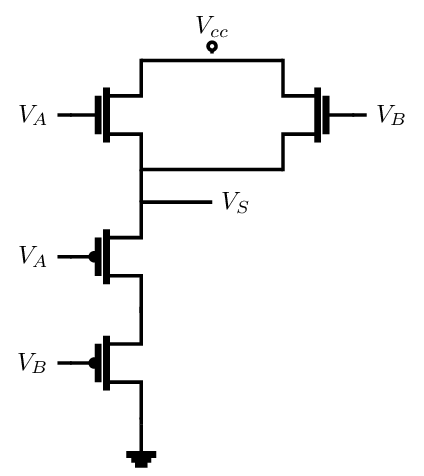
Porte NOR : \(S = \overline{A+B}\)

1. Une réalisation possible d’une porte NOR en technologie CMOS.
   
2. Symbole normalisé.

On essaye une OR : \(S = A+B\)

On essaye une OR : \(S = A+B\)

On fait comment ??

car \(A+B = \overline{\overline{A}.\overline{B}} = \overline{\overline{A.A}.\overline{A.A}}\).

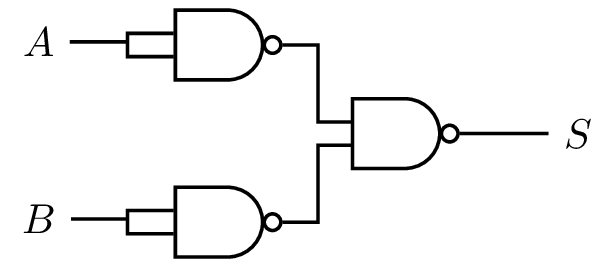
Universalité de la porte NAND

Lois de DeMorgan

• \(\overline{A.B} = \overline{A} + \overline{B}\)
• \(\overline{A+B} = \overline{A}.\overline{B}\)

On peut construire les portes AND, OR, NOT à partir de NAND.

La porte NAND est dite universelle.

La couche logique : logique combinatoire

Portes logiques

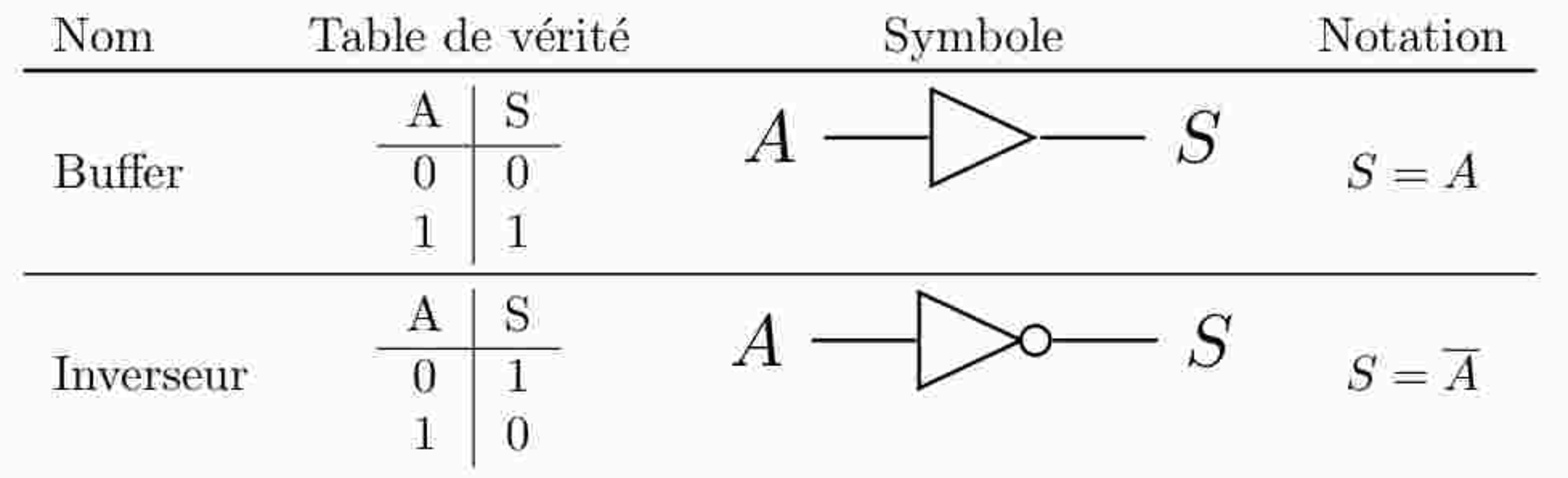
Portes à 1 entrée

Portes à 2 entrées

Synthèse de circuits logiques

Les outils

• Spécification fonctionnelle : table de vérité (e.g. \(A + B\))
• Équation logique et simplification (Tableau de Karnaugh) (e.g. \(A + B\))
• Disjonction de conjonctions
• peut être réalisé
  • exclusivement avec des NAND,
  • ou exclusivement avec des NOR
  • exclusivement avec des NOT, AND, OR

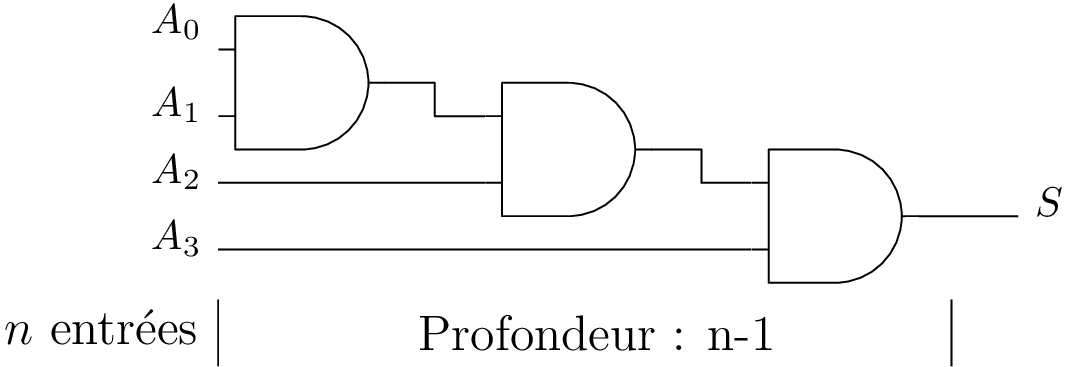
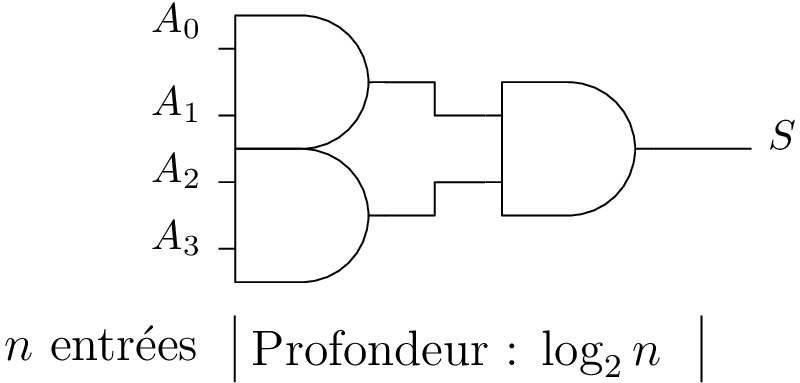
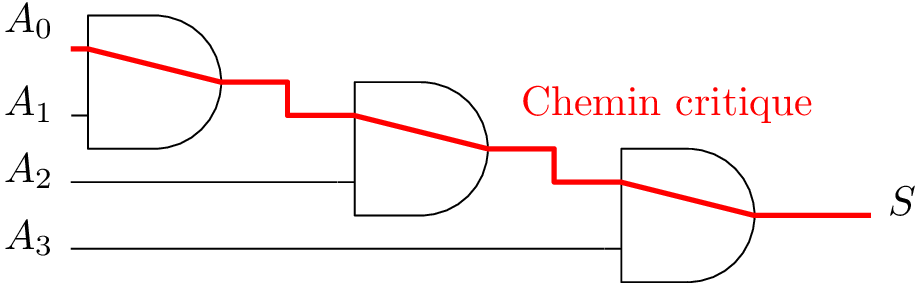
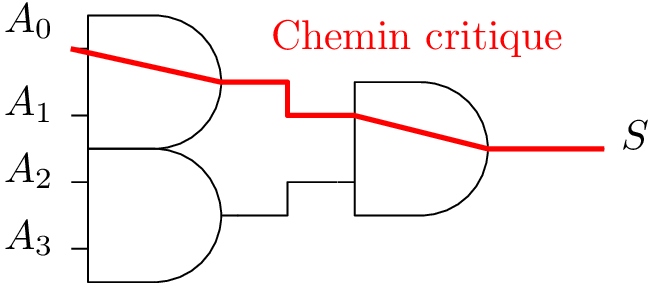
Circuits à \(n > 2\) entrées

Exemple d’une porte ET à 4 entrées.

Le chemin critique définit le temps de propagation :

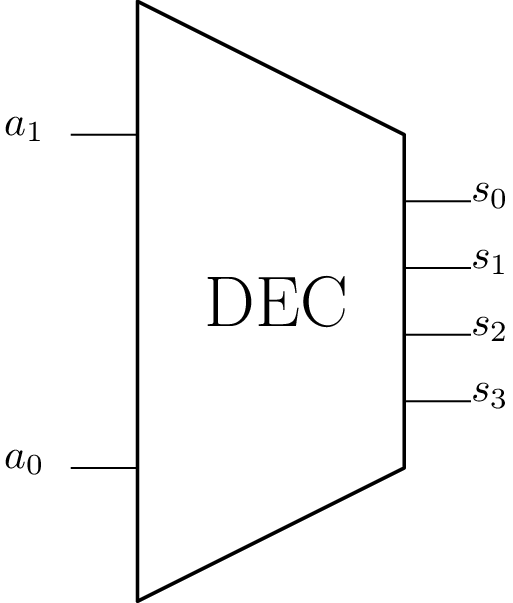
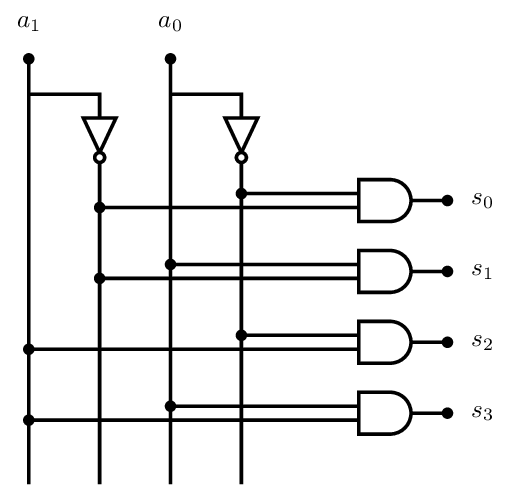
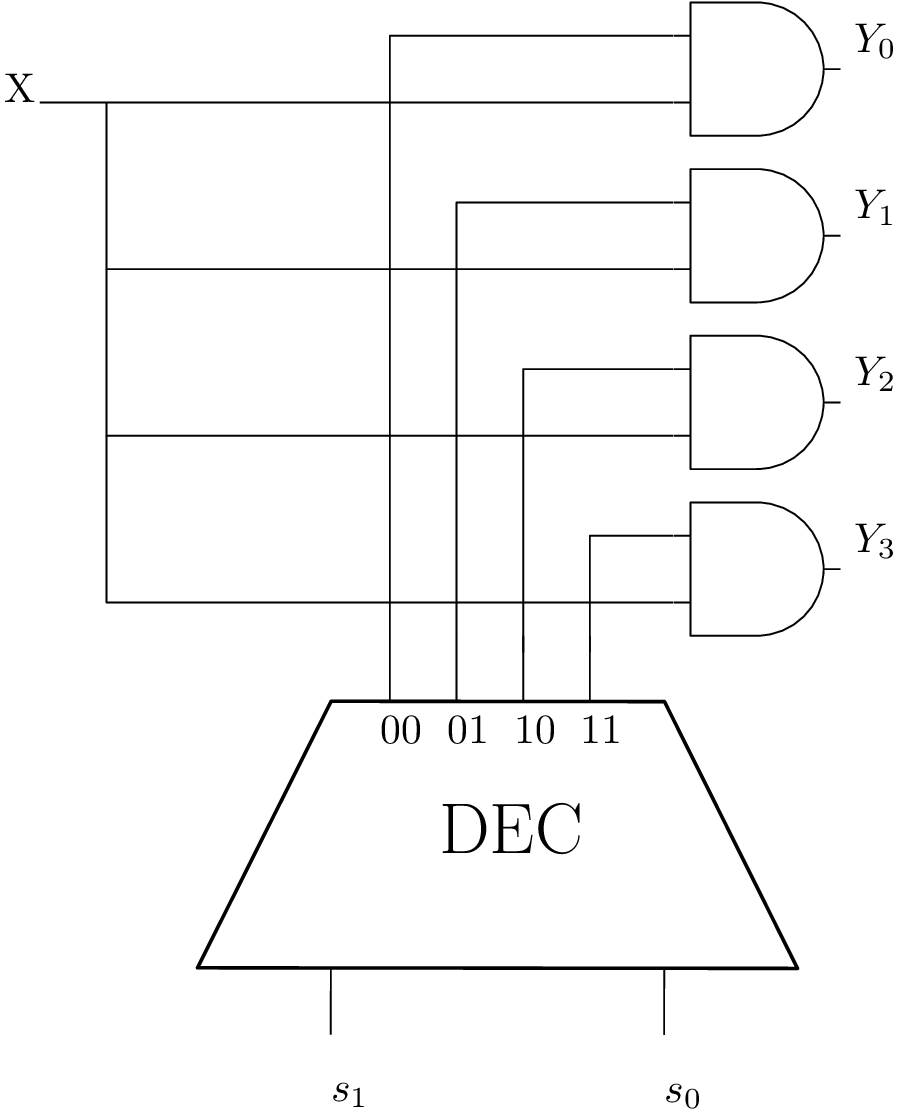
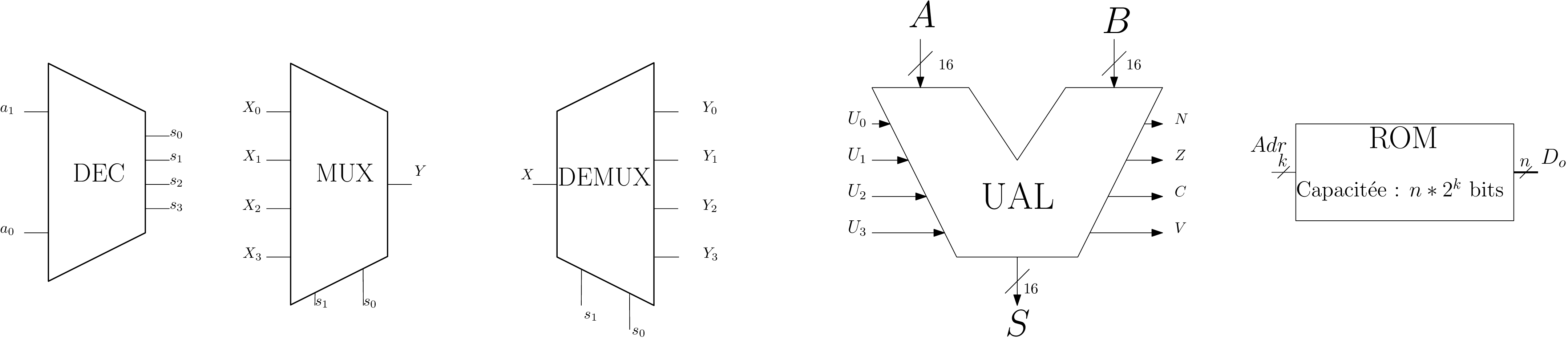
Circuits de logique combinatoire : Décodeur

⇒ Spécification fonctionnelle

Symbole

Circuit

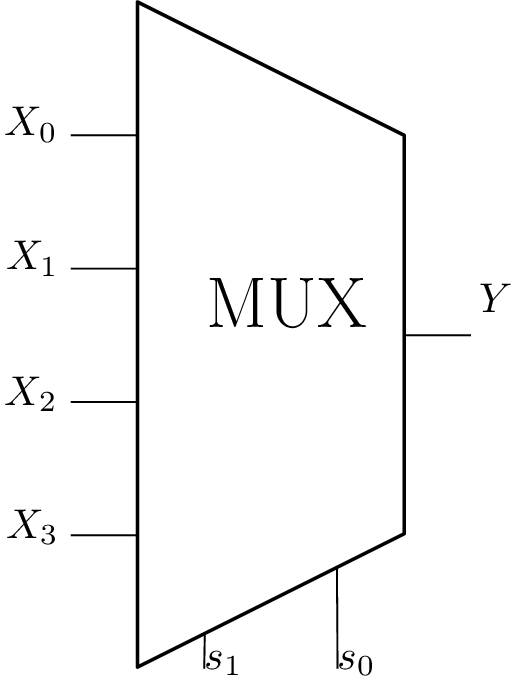
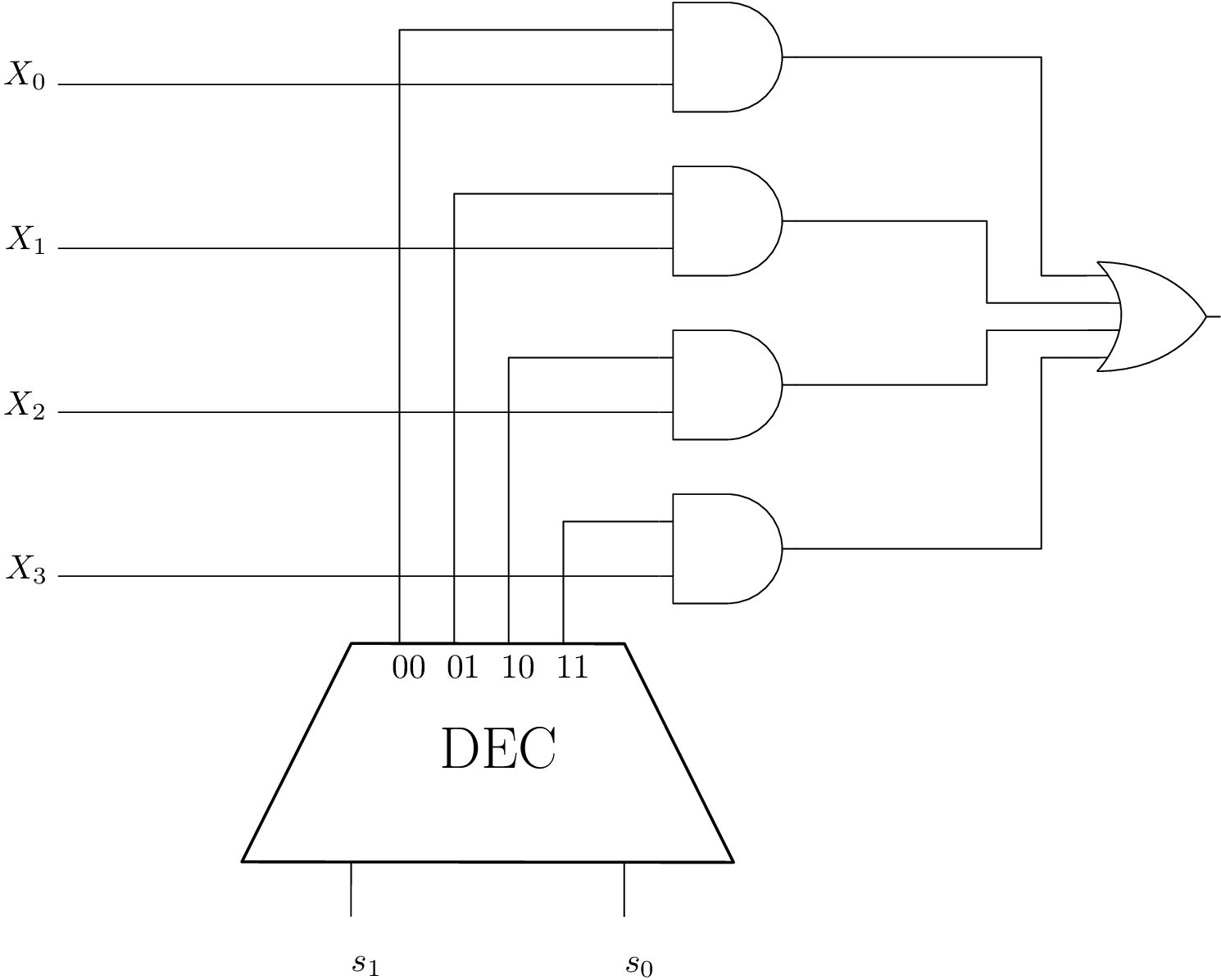
Circuit de logique combinatoire : Multiplexeur

⇒ Spécification fonctionnelle

Multiplexeur

Circuit multiplexeur

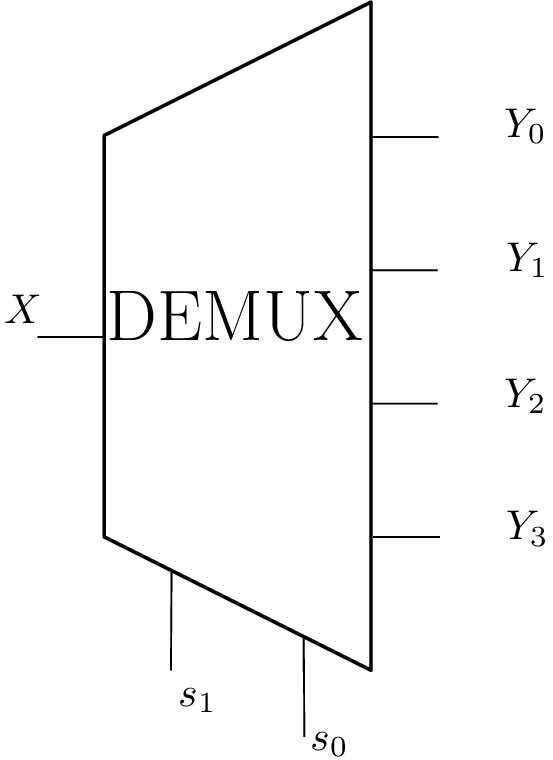
Circuit de logique combinatoire : Démultiplexeur

⇒ Spécification fonctionnelle

Démultiplexeur

Circuit démultiplexeur

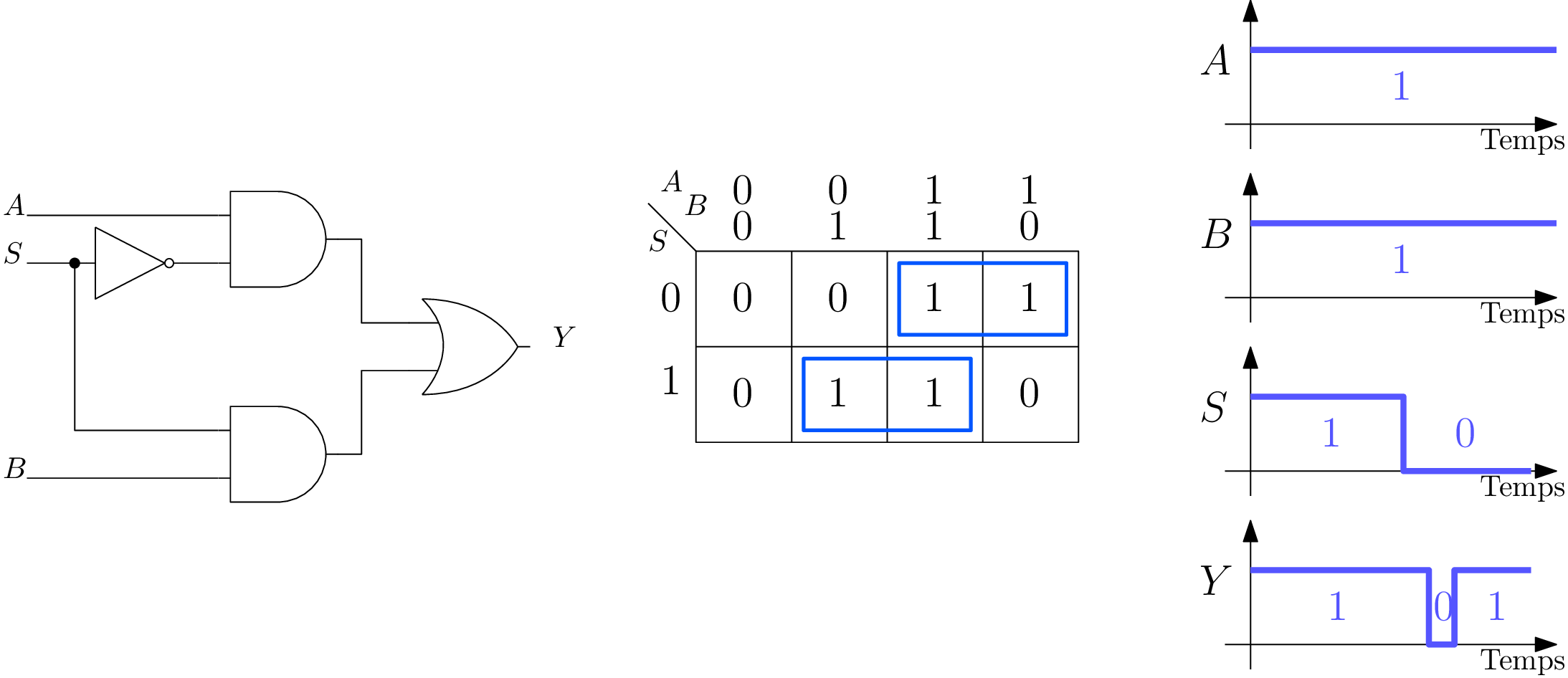
Aléa statique

Quel est le problème ? Example du multiplexeur.

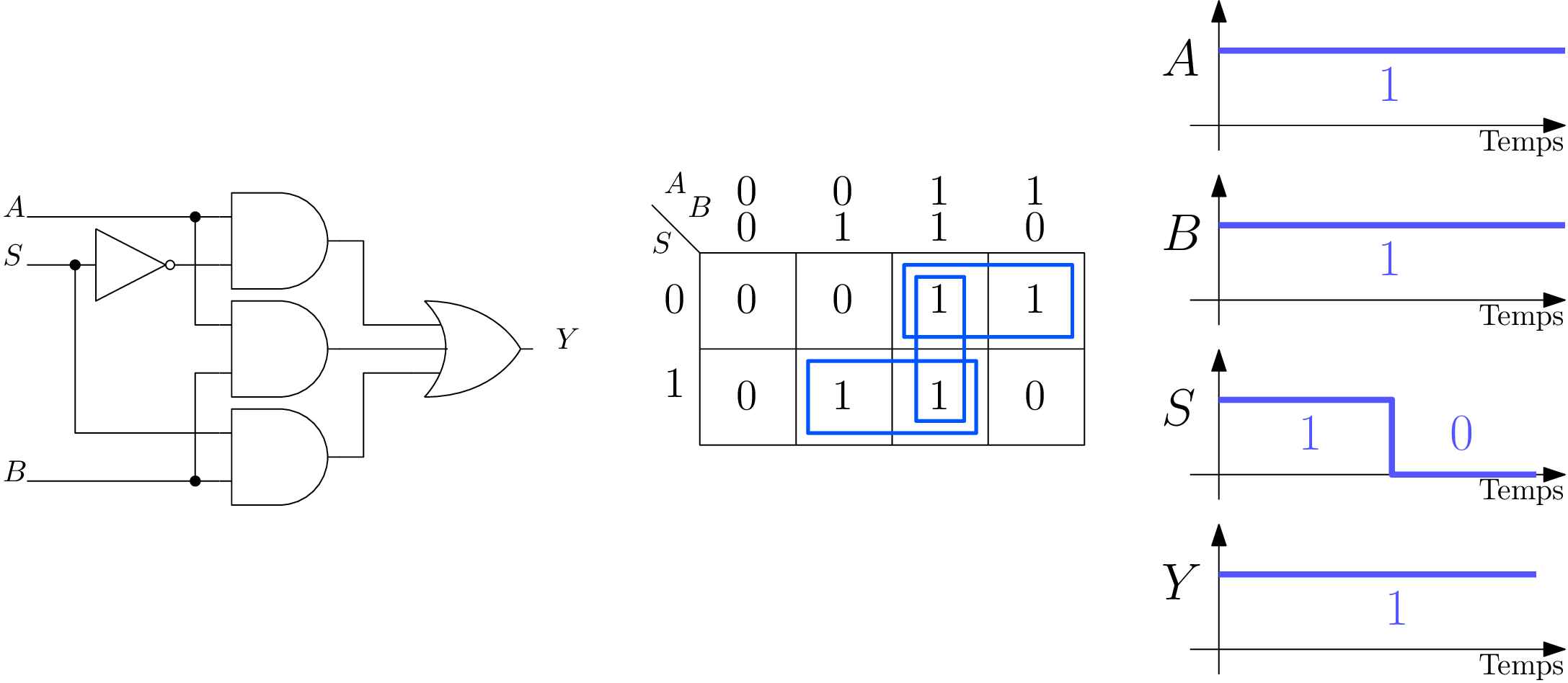
Supprimer ce changement transitoire.

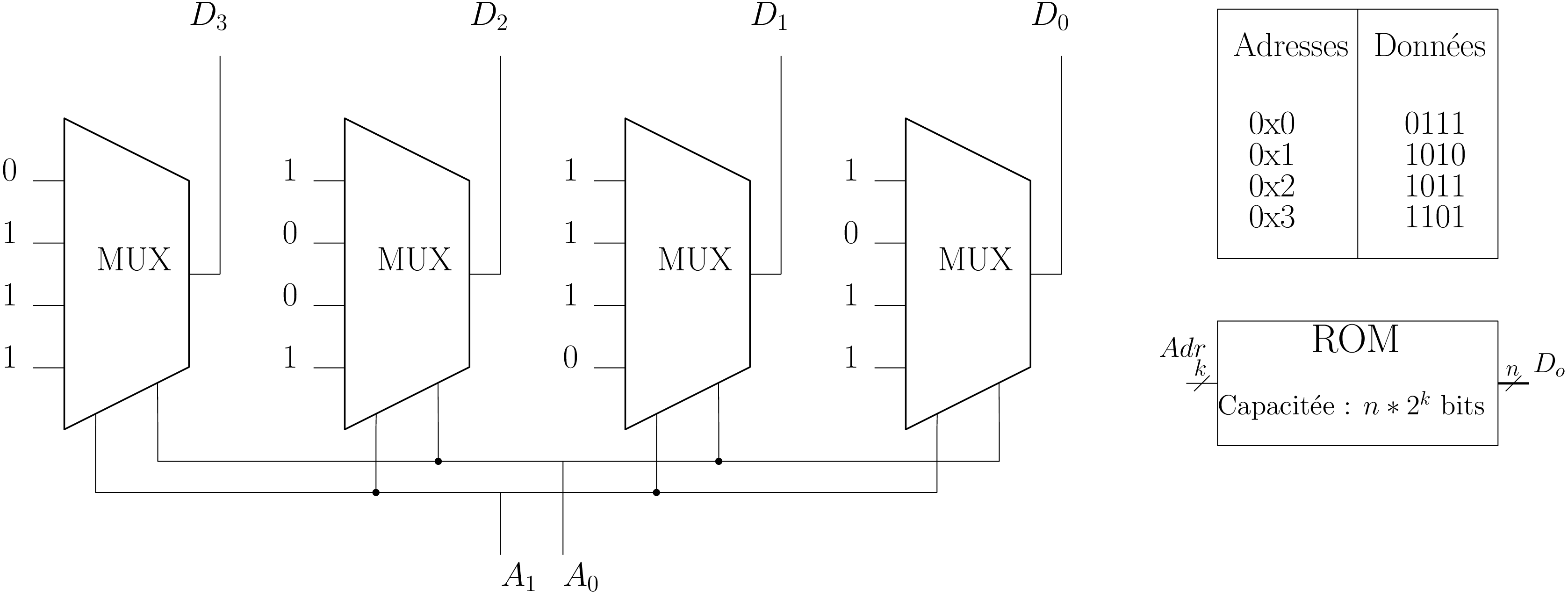
Universalité du multiplexeur et Read Only Memory ROM

AND avec MUX

AND avec MUX 2

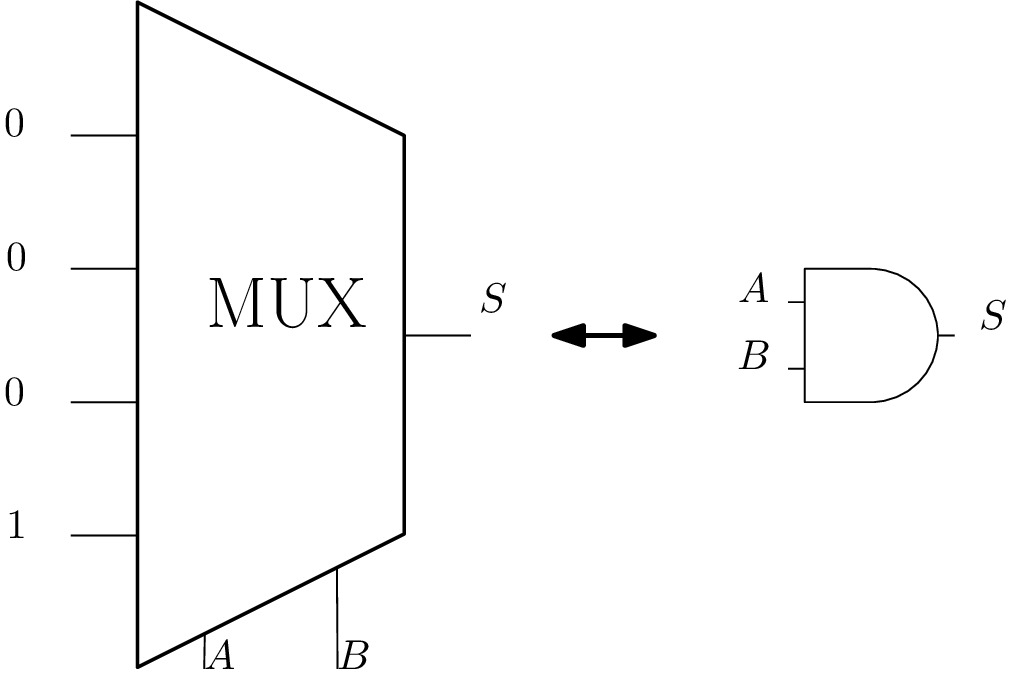
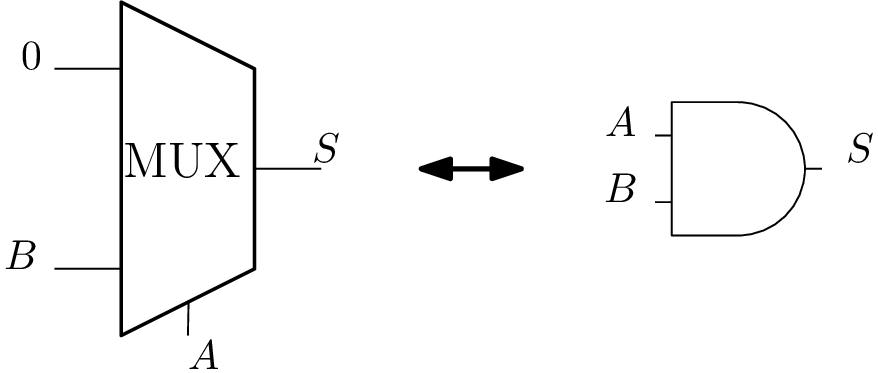
⇒ Read Only Memory (ROM)

Mémoire en lecture seule (ROM - Read Only Memory)

Unité arithmétique et logique (UAL) : Cahier des charges

• composant logique avec :
  • 2 entrées A, B sur \(n\) bits
  • 1 sortie S sur \(n\) bits
  • des bits de sélection d’opération, e.g. \(2^4 = 16\) op: \(U_3U_2U_1U_0\)

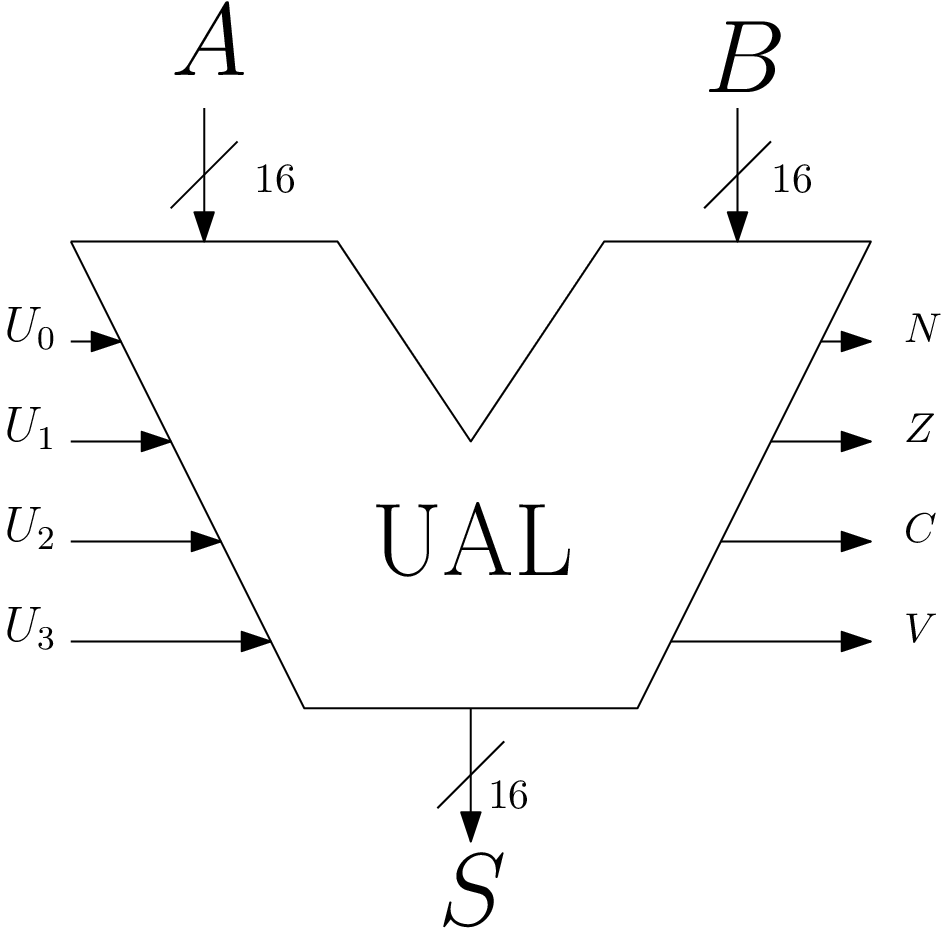
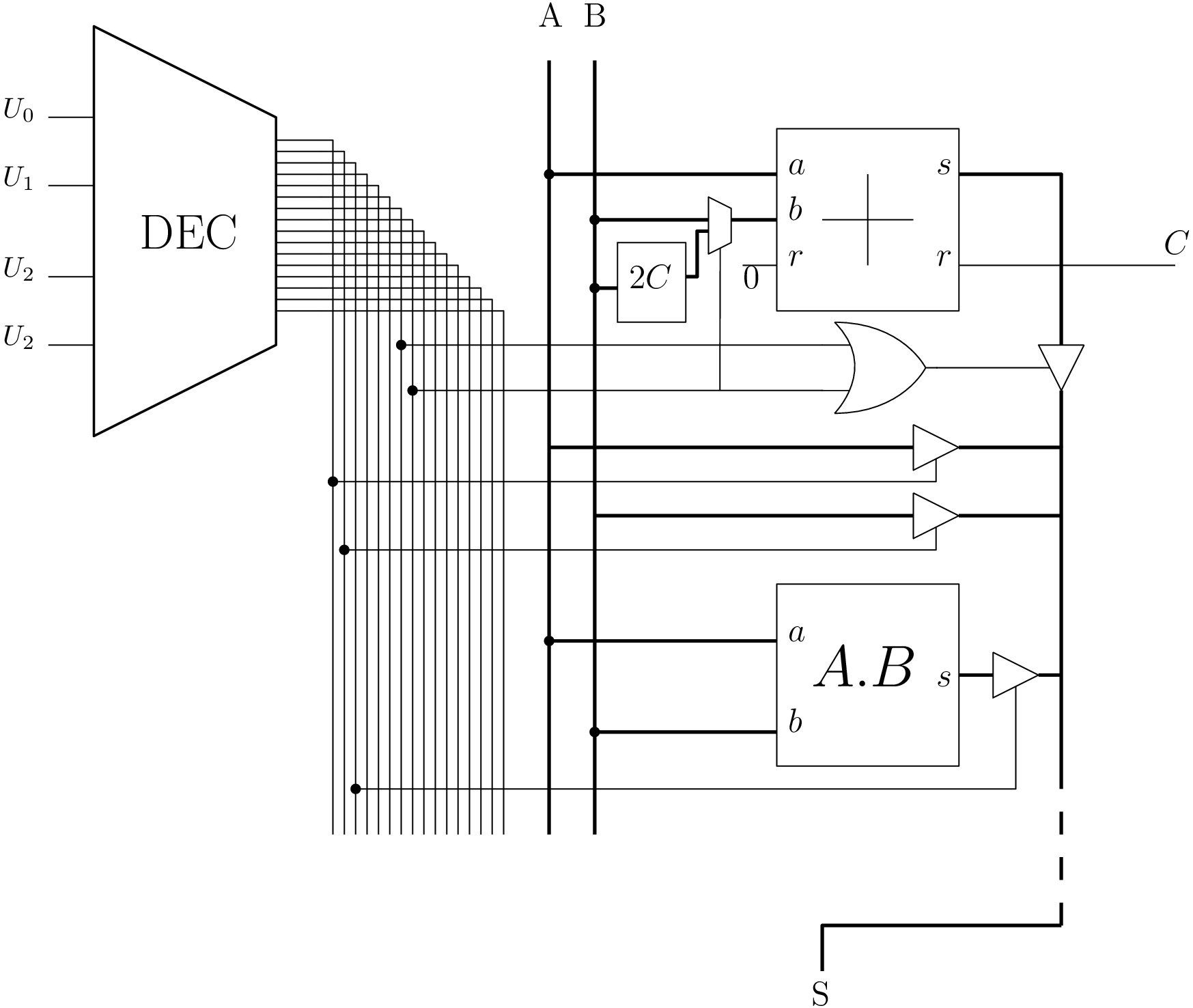
UAL

UAL - Additionneur

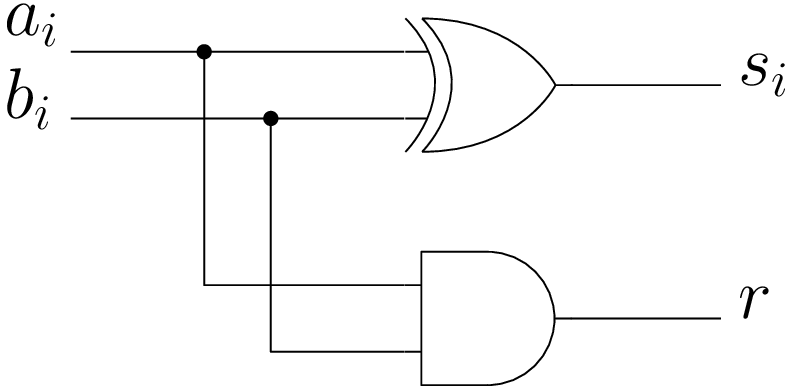
Demi-additionneur 1 bit

Table de vérité :

\(a_i\)	\(b_i\)	\(s_i\)	\(r\)
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Circuit :

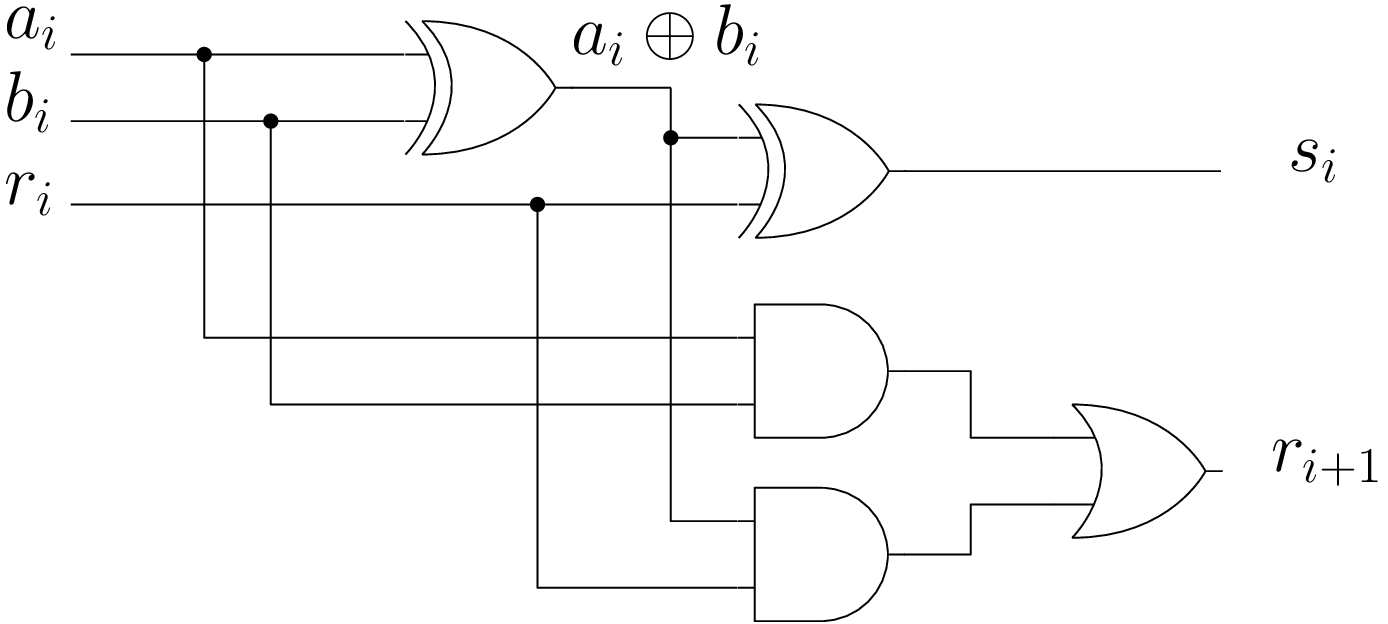
Additionneur 1 bit

Table de vérité :

\(a_i\)	\(b_i\)	\(r_i\)	\(s_i\)	\(r_{i+1}\)
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Circuit :

Additionneur

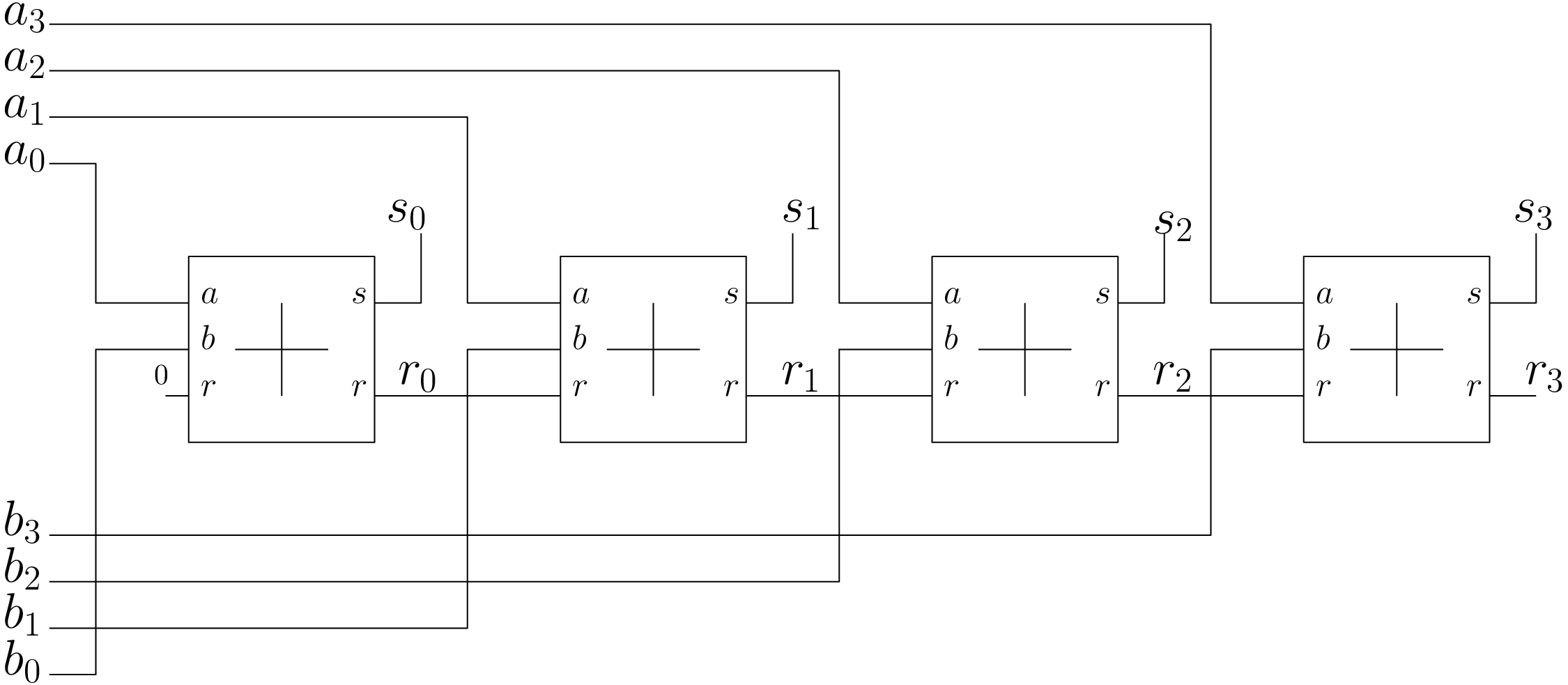
Additionneur n bits

Synthèse de l’UAL

• on réalise chacun des circuits opératoires
• on les combine et sélectionne grâce à un décodeur

Résumons

Logique combinatoire

Pour réaliser un circuit de logique combinatoire

• spécification fonctionnelle : table de vérité, équation logique
• simplification de l’équation (e.g. tableaux de karnaugh)
• circuit avec les portes logiques ET, OU, NOT (ou juste NAND, NOR, MUX)

Par exemple

Circuits logique combinatoire

La couche logique : logique séquentielle

C’est tout ?

Problème : un bouton (0/1) - une lumière (0/1)

Allumons

Éteignons

⇒ mince ?!?!

Solution

Problème : un bouton (0/1) - une lumière (0/1)

Solution

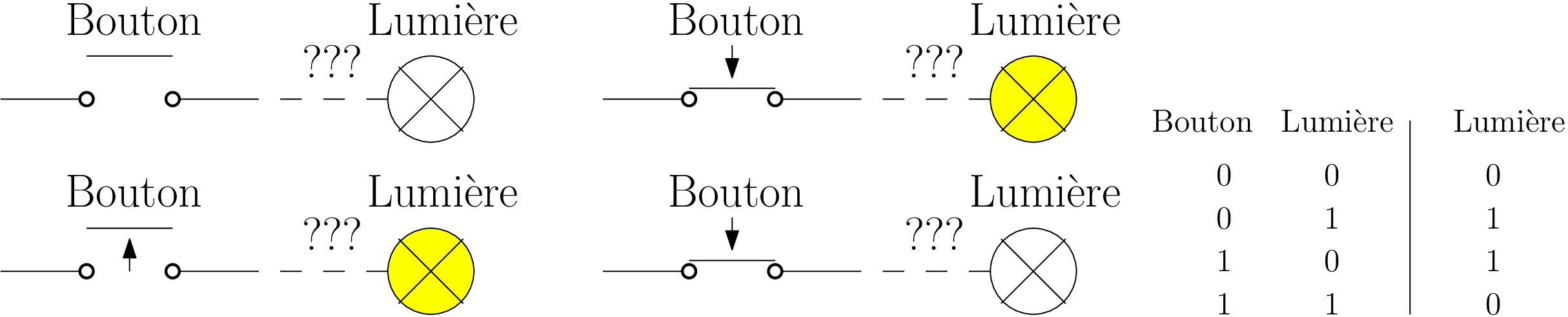
Le nouvel état lumière dépend de l’entrée bouton et de l’ancien état lumière.

Ici, la sortie est caractéristique de l’état du système.

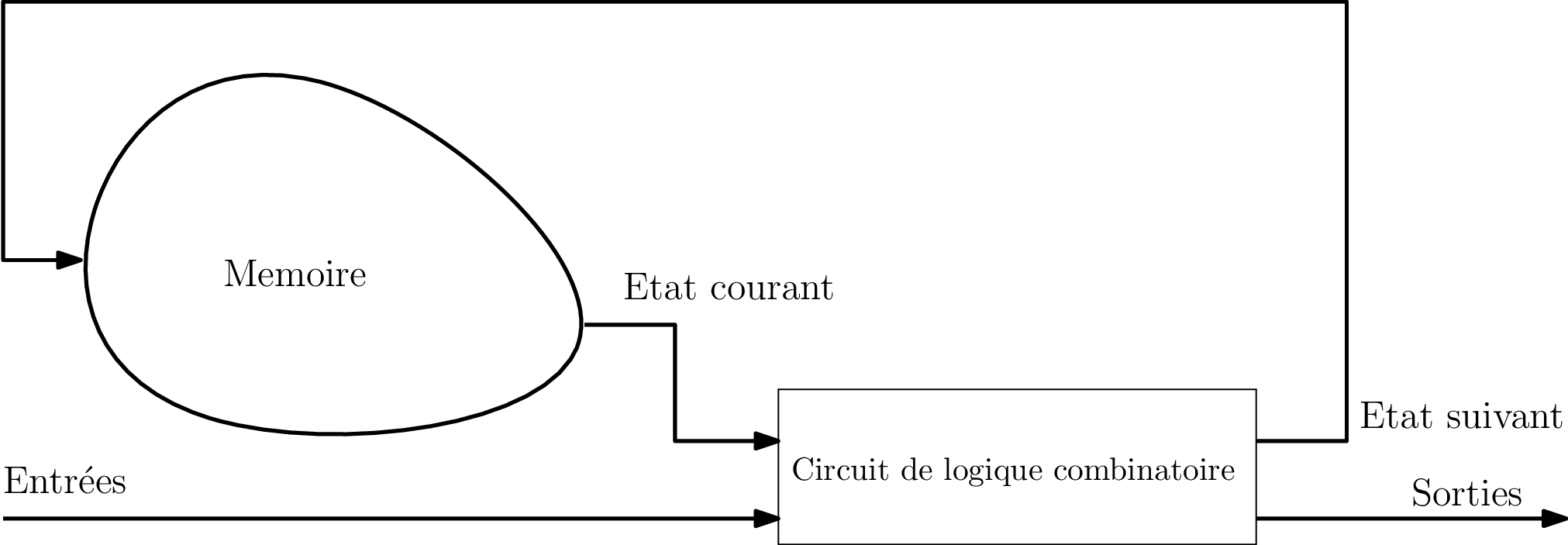
Plus généralement : logique séquentielle

On reboucle simplement la sortie sur l’entrée ?

Ce n’est pas forcément la sortie qui est utilisée en entrée puisque je peux très bien avoir besoin de produire la même sortie dans des états différents

Transducteur fini (automate fini avec sorties)

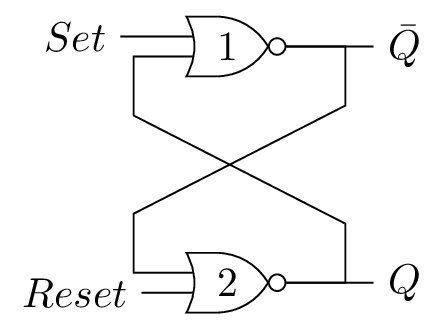
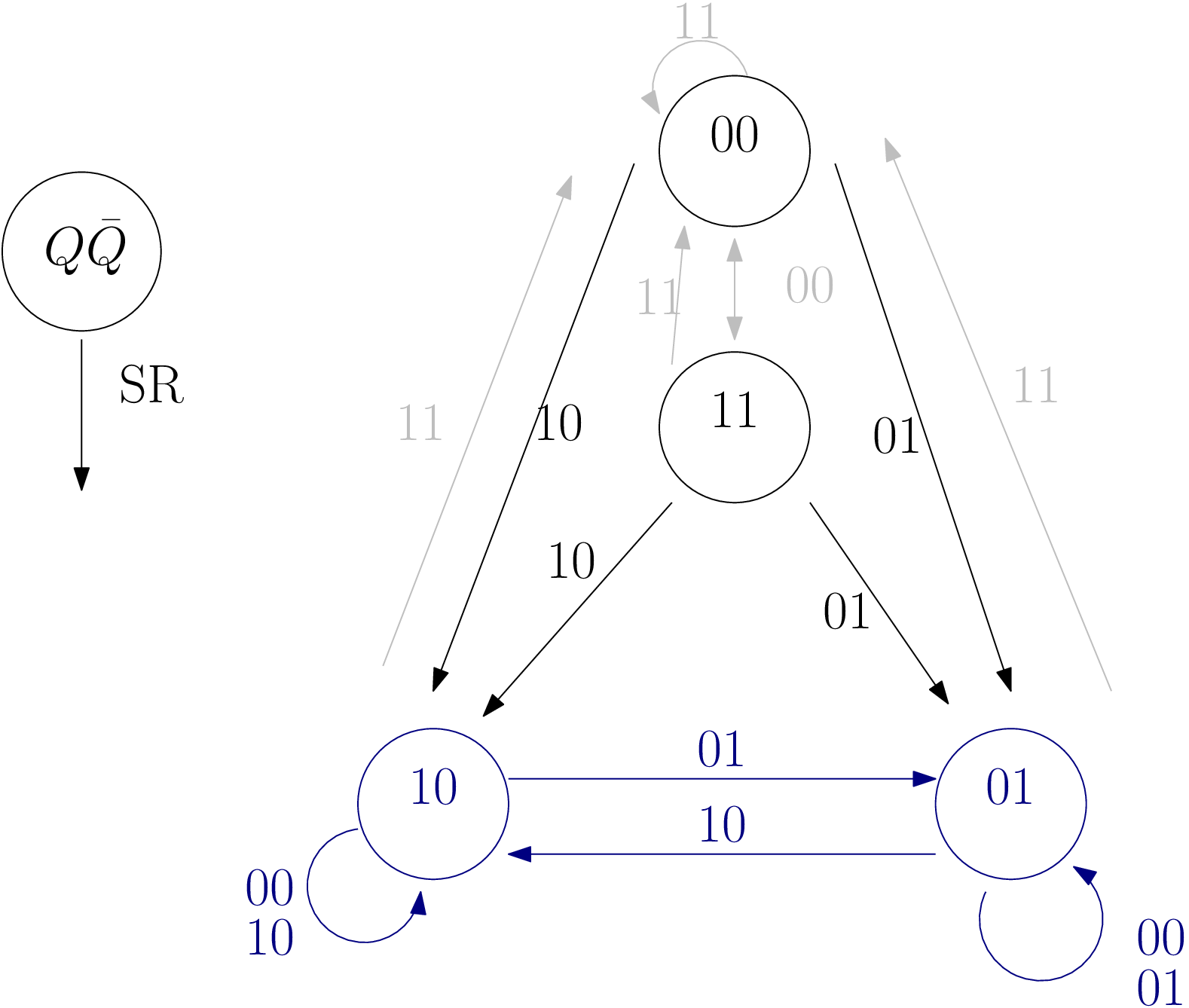
Verrou Reset-Set (RS)

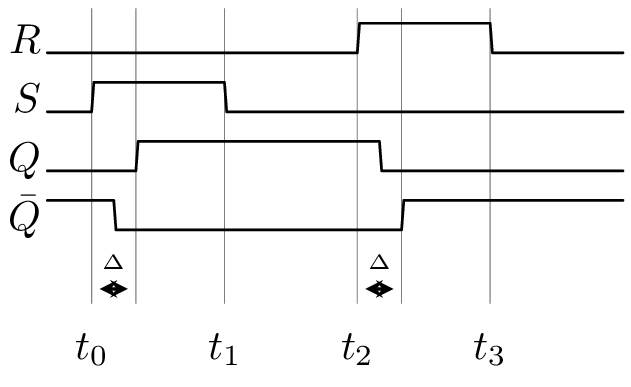
Schéma et Chronogramme

Verrou RS circuit

Chronogramme RS

• \((S,\bar{R})\) fait transiter et rester à l’état \((Q, \bar{Q}) = (1,0)\)
• \((\bar{S},R)\) fait transiter et rester à l’état \((Q, \bar{Q}) = (0,1)\)
• \((\bar{S}, \bar{R})\) effet mémoire

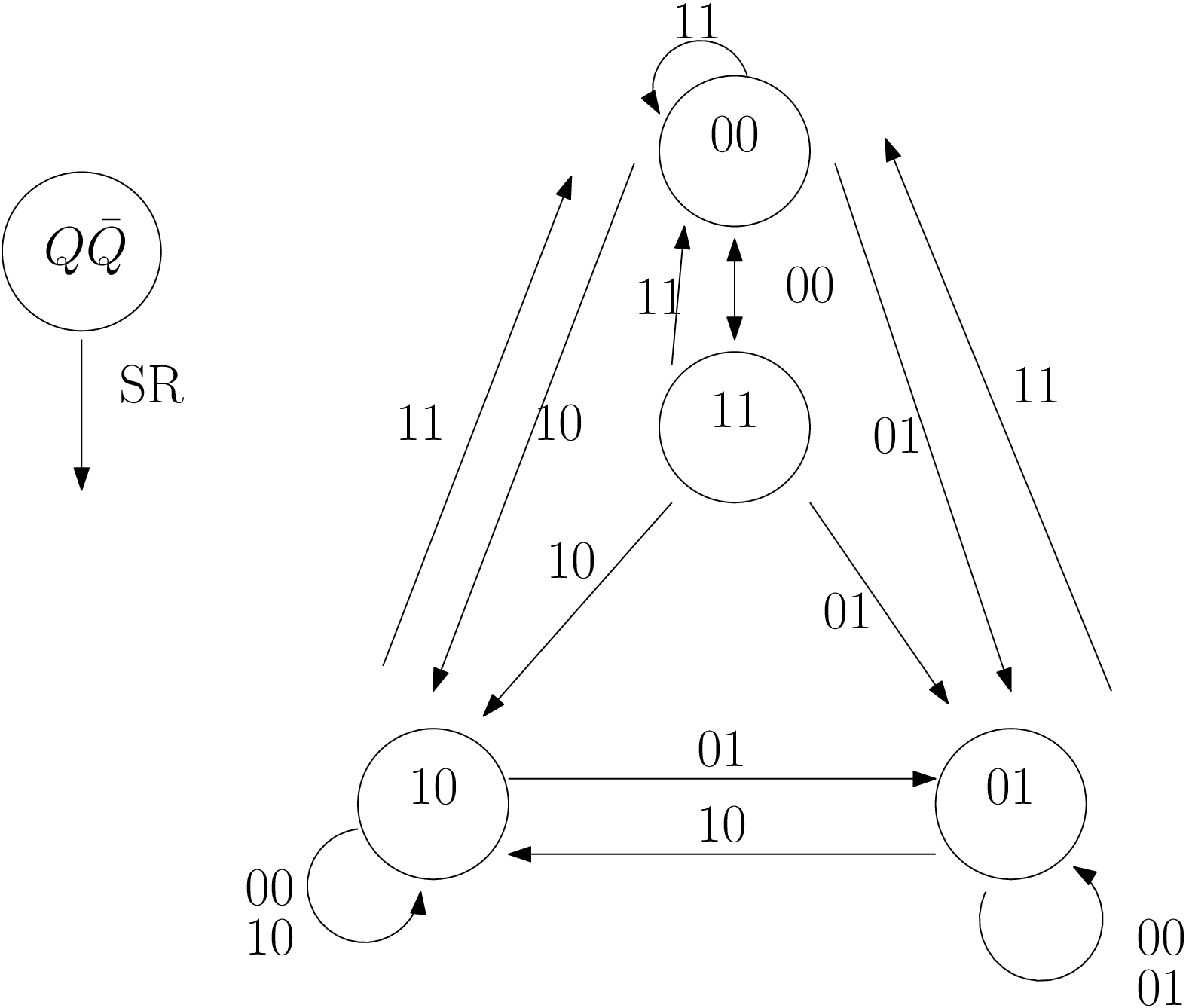
En fait … c’est plus compliqué : Machine à états finis pour un circuit symétrique

Verrou RS circuit

FSM RS

Supprimer les états instables

Et si \(R.S = 0\) ?

Verrou RS circuit

FSM RS complet

Mémoriser un bit sur niveau haut : Verrou D

Schéma et chronogramme

On présente une donnée \(D\) écrite sur niveau haut \(Enable\).

Circuit verrou D

Symbole verrou D

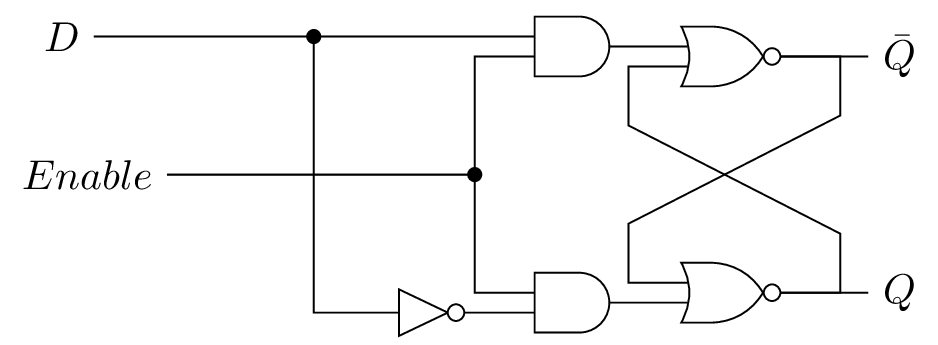
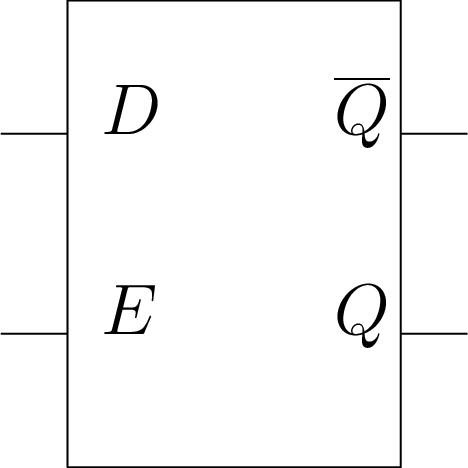
Important

• \(Set = D \cdot Enable\)
• \(Reset = \overline{D} \cdot Enable\)
• \(Q(t) = Enable \cdot D + \overline{Enable} \cdot Q(t-1)\)

Chronogramme du verrou D

Symbole verrou D

Chronogramme verrou D

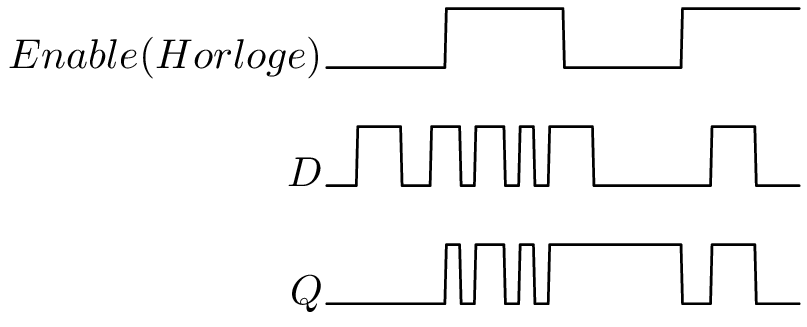
Important

• \(E=1 \Rightarrow Q = D\) : le verrou est transparent,
• \(E=0 \Rightarrow\) le verrou est dans un état mémoire, sa sortie ne change pas même si \(D\) change

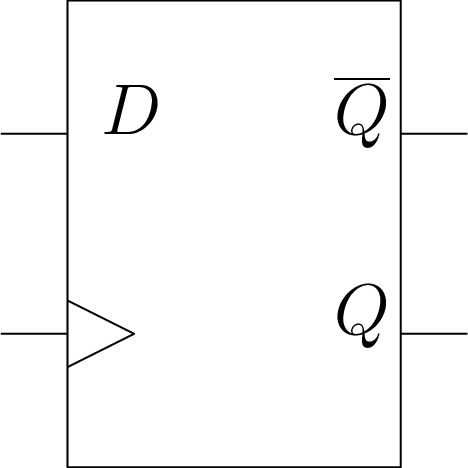
Mémoriser un bit sur un front : Bascule D

Bascule D : maître-esclave; Schéma et chronogramme

Bascule D

Chronogramme bascule D

Schéma bascule D

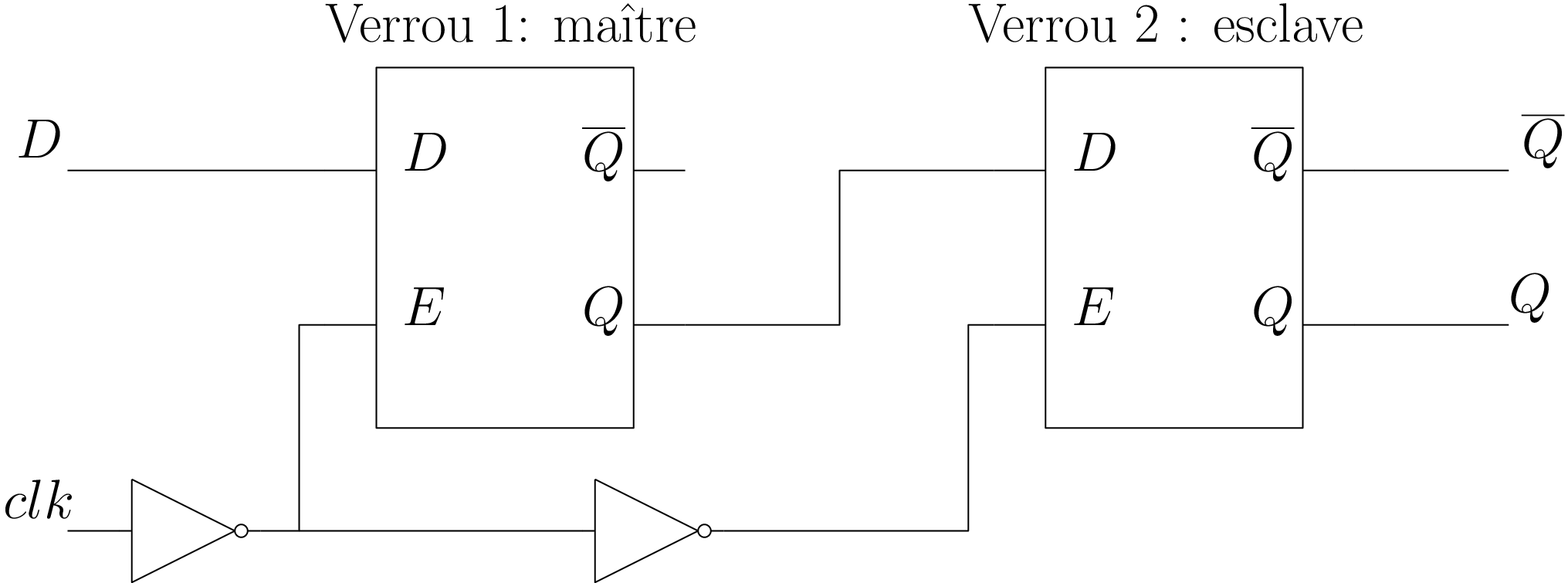
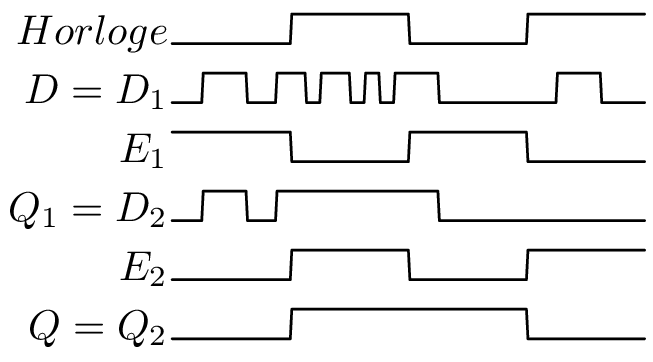
\(Q=D\) au front montant d’horloge

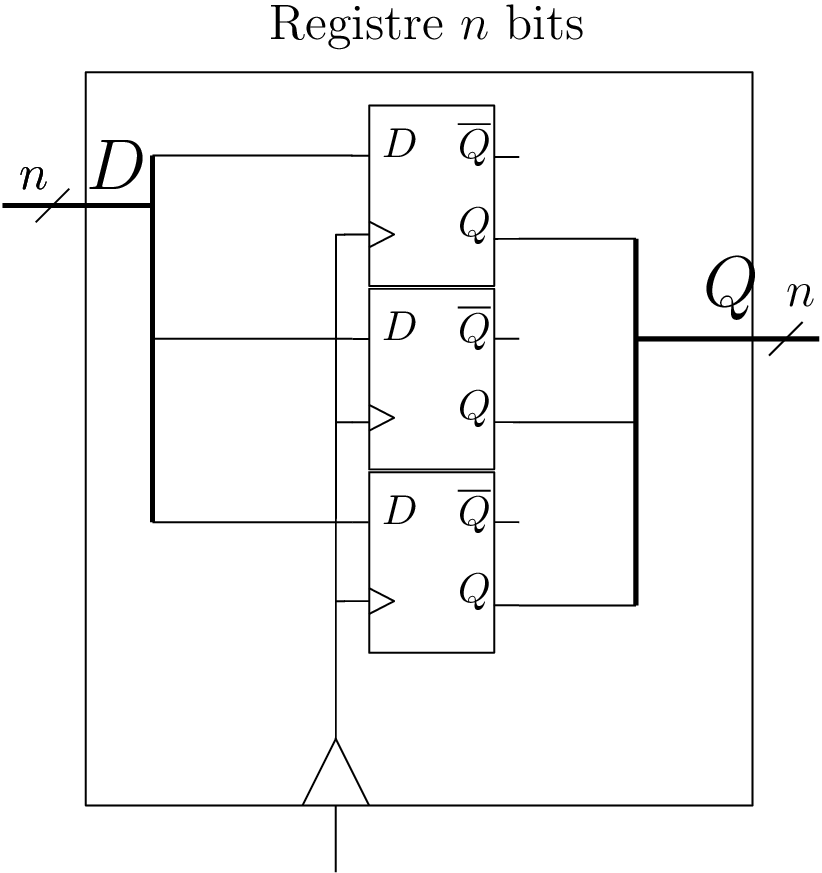
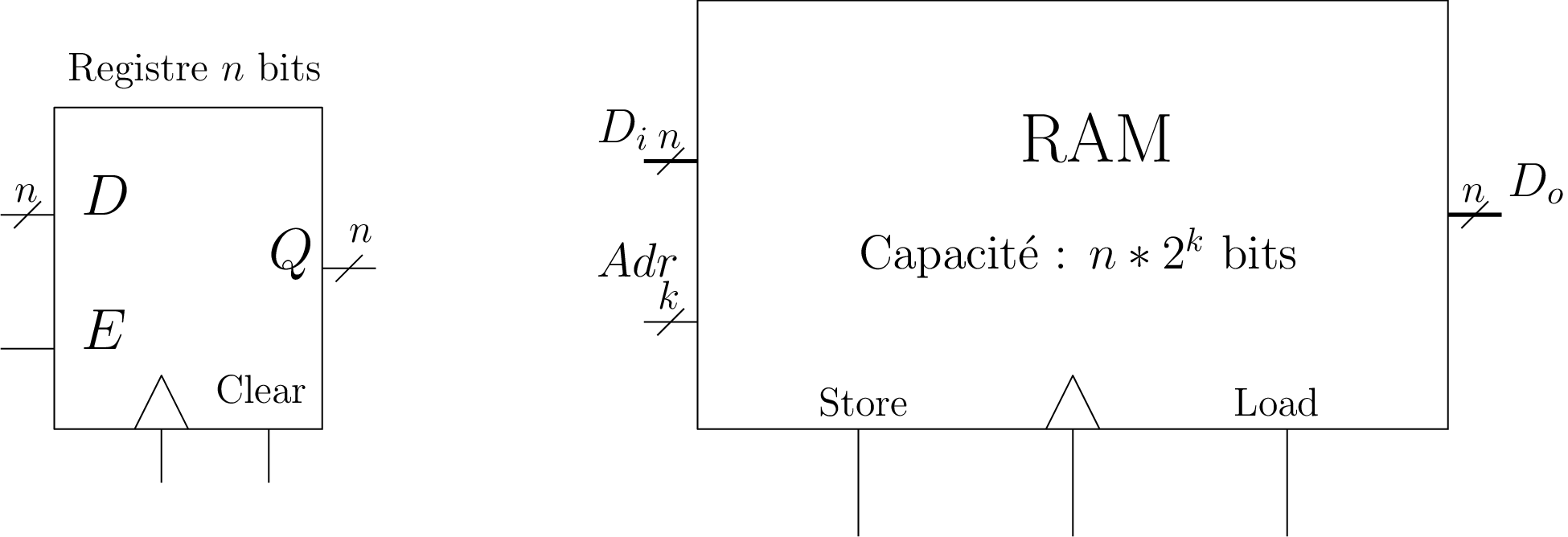
Registre à \(n\) bits

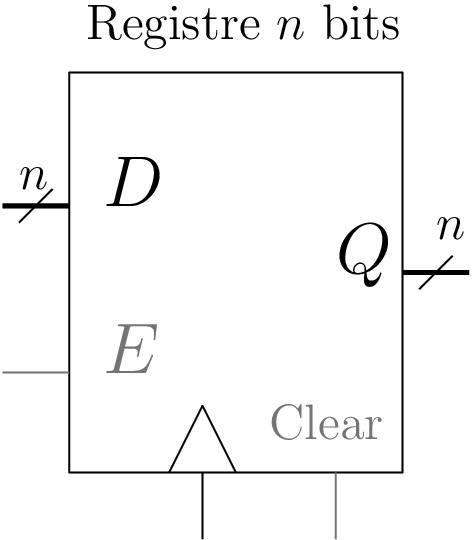
Mémoire Random Access Memory RAM

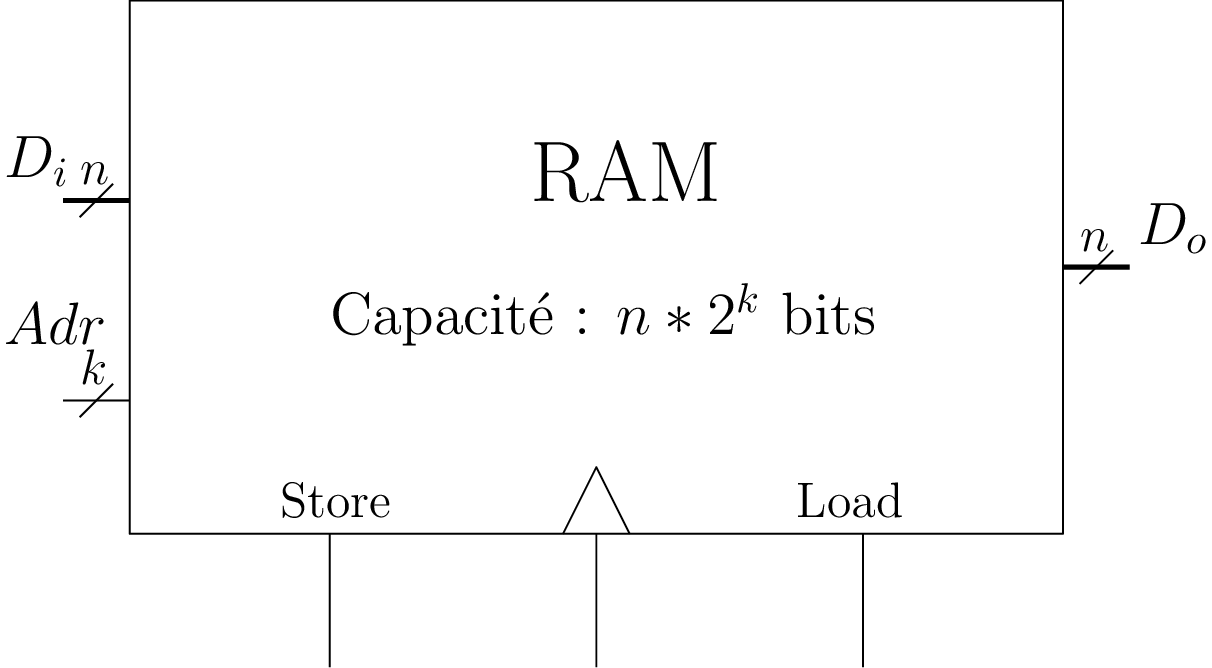
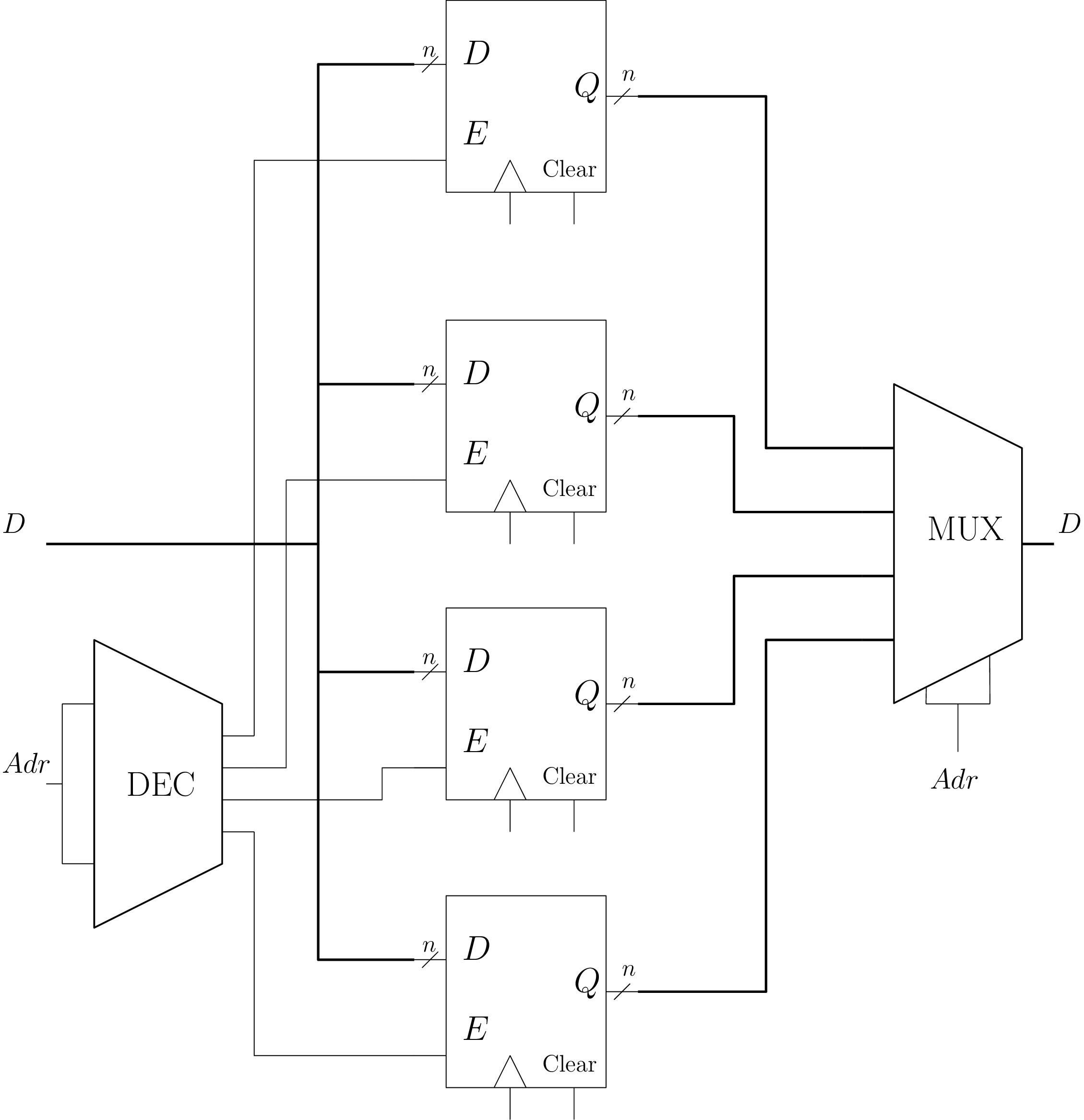
• Lecture : on place Adr et Load=1 ⇒ \(D_o\) = RAM[Adr]
• Écriture : on place Adr, \(D_i\) et Store=1 + front d’horloge ⇒ RAM[Adr] = \(D_{i}\)

Résumons

Logique combinatoire

Logique séquentielle

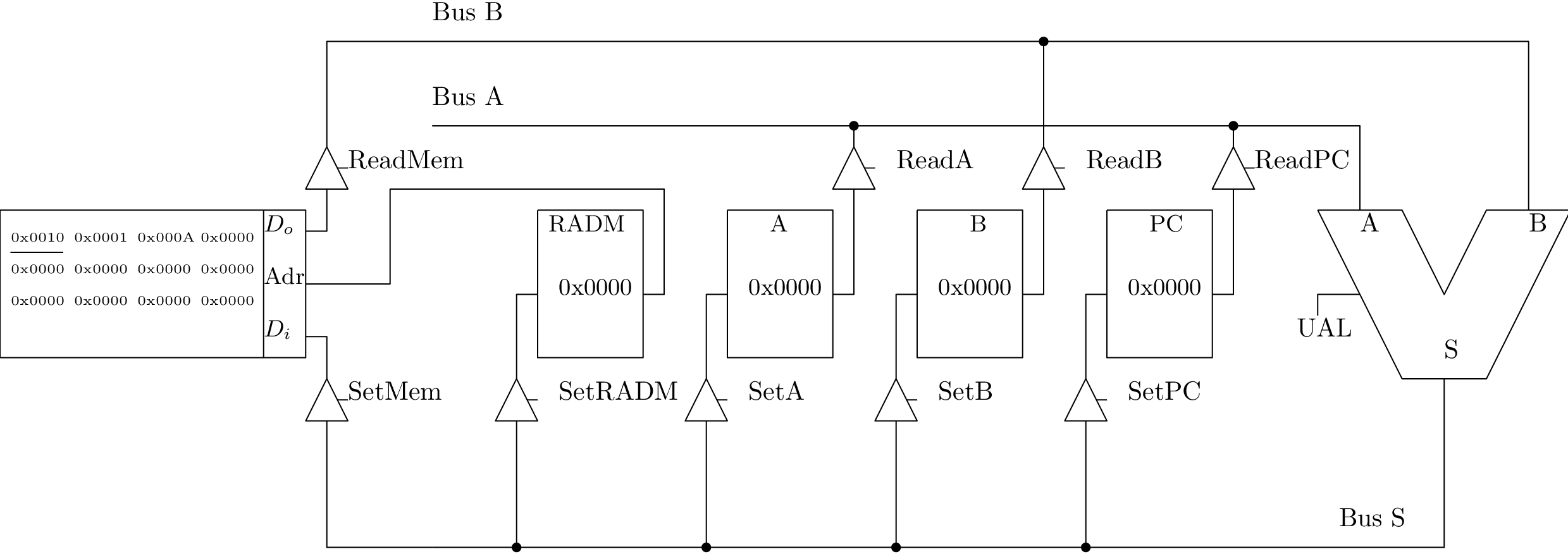
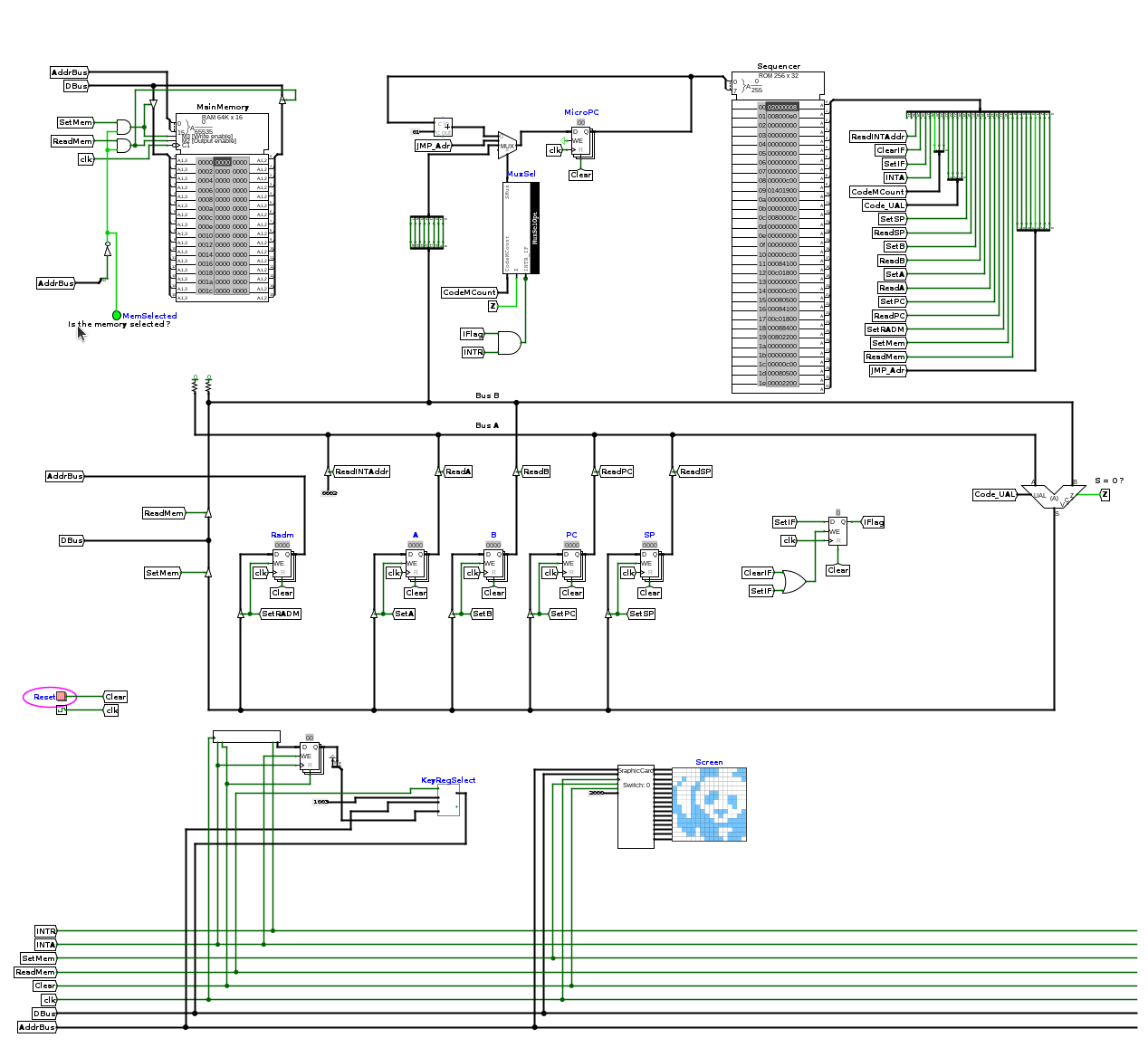
Notre premier chemin de données

Notre premier chemin de données

Premier chemin

Spécifications

• données et adresses sur 16 bits; RAM : \(2^{16}\) mots de 16 bits = 128 ko
• des registres génériques : A, B ; des registres particuliers PC et RADM
• RAM pour stocker (pour le moment) les données
• des signaux de contrôle : Read<A,B,PC,Mem>, Set<A,B,PC,RADM,Mem>, UAL
• Architecture Register/Register (Load/Store) : opérations avec des opérandes en registres

Voir cette comparaison d’architectures ISA pour de vrais examples.

Les registres

Premier chemin

• A, B : registres d’opérandes pour effectuer des opérations (general purpose)
• PC (Program counter, ou CO : compteur ordinal): index la position de la donnée en cours d’utilisation
• RADM : Registre d’Adresse Mémoire : quel mot est adressé en mémoire (≠ PC)

Exemple de séquencement manuel

Problème

Additionner 16=0x0010 et 1=0x0001 et stocker le résultat à l’adresse 0x000A

Adresses de base	Contenu
0x0000	0010	0001	000A	0000
0x0004	0000	0000	0000	0000
0x0008	0000	0000	0000	0000

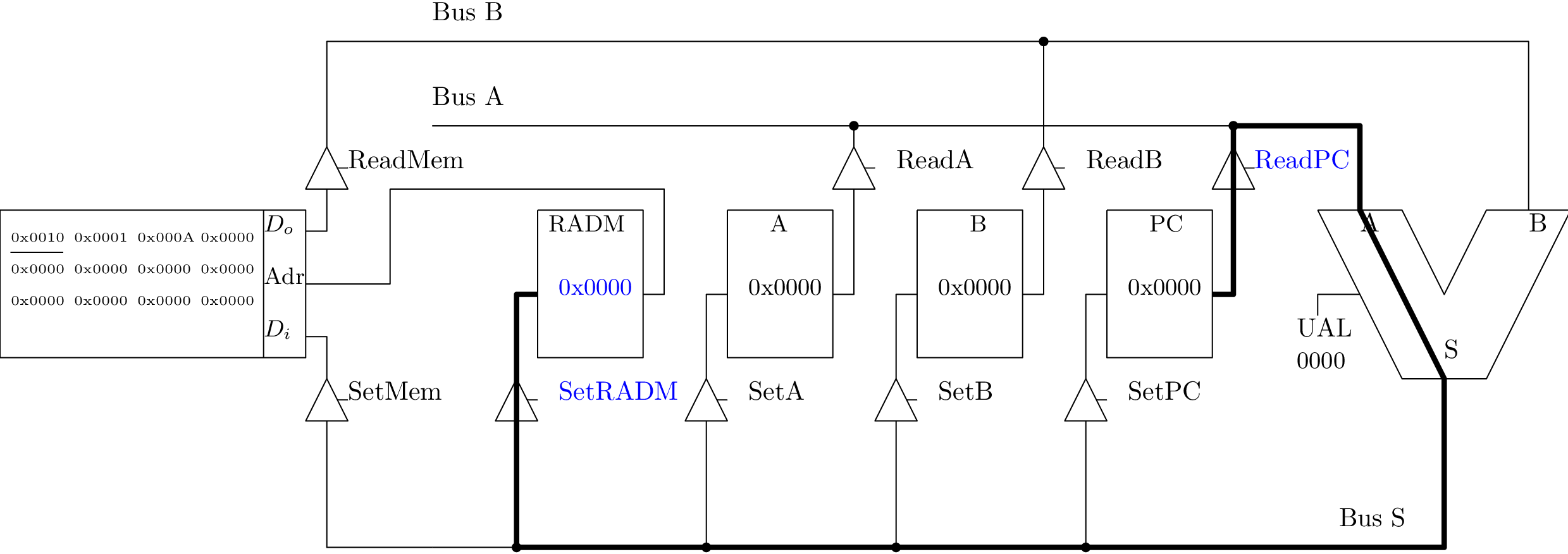
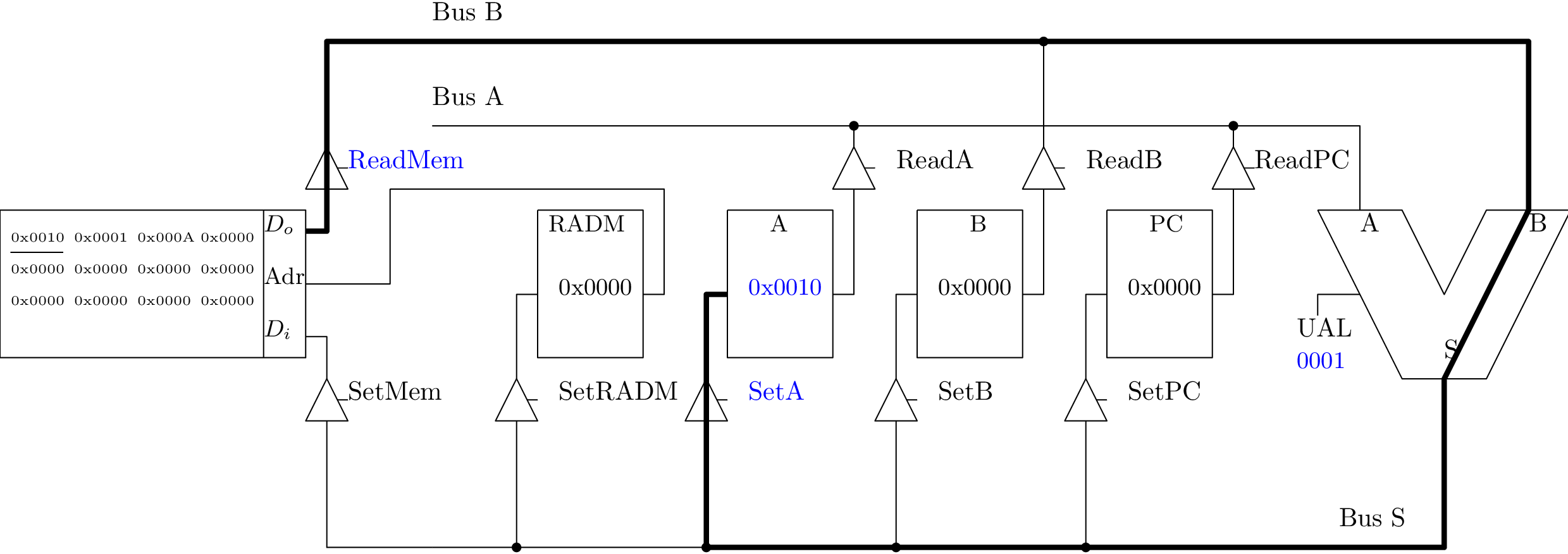
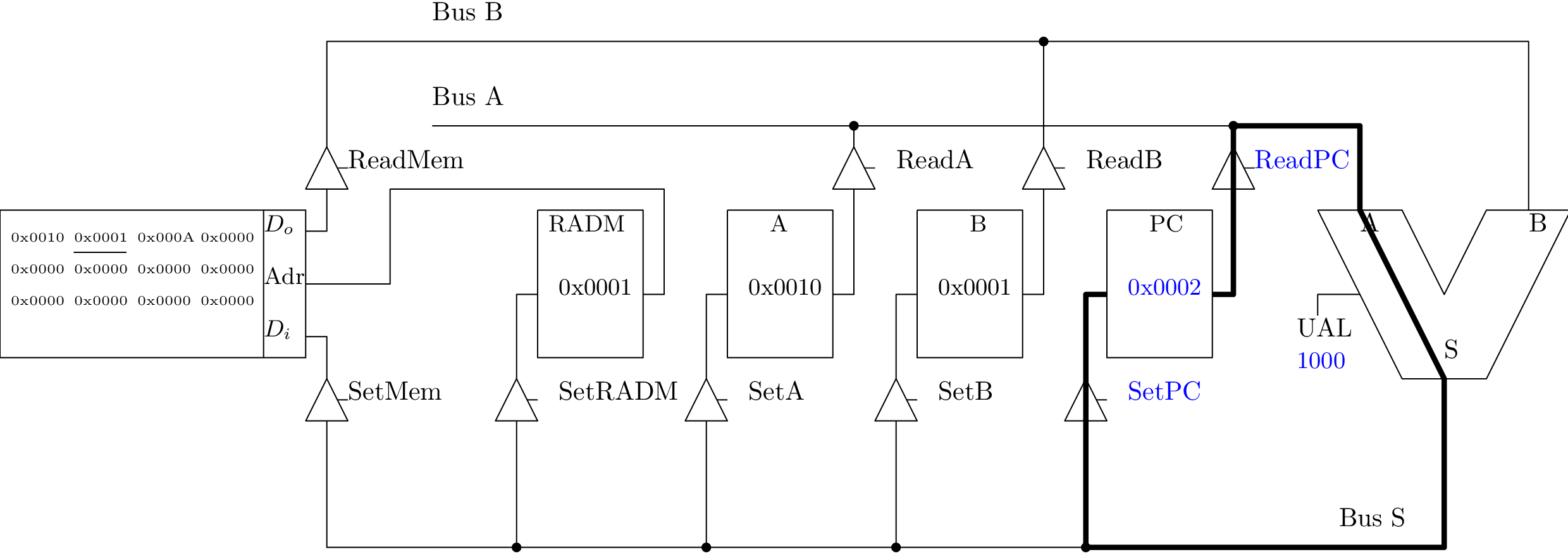
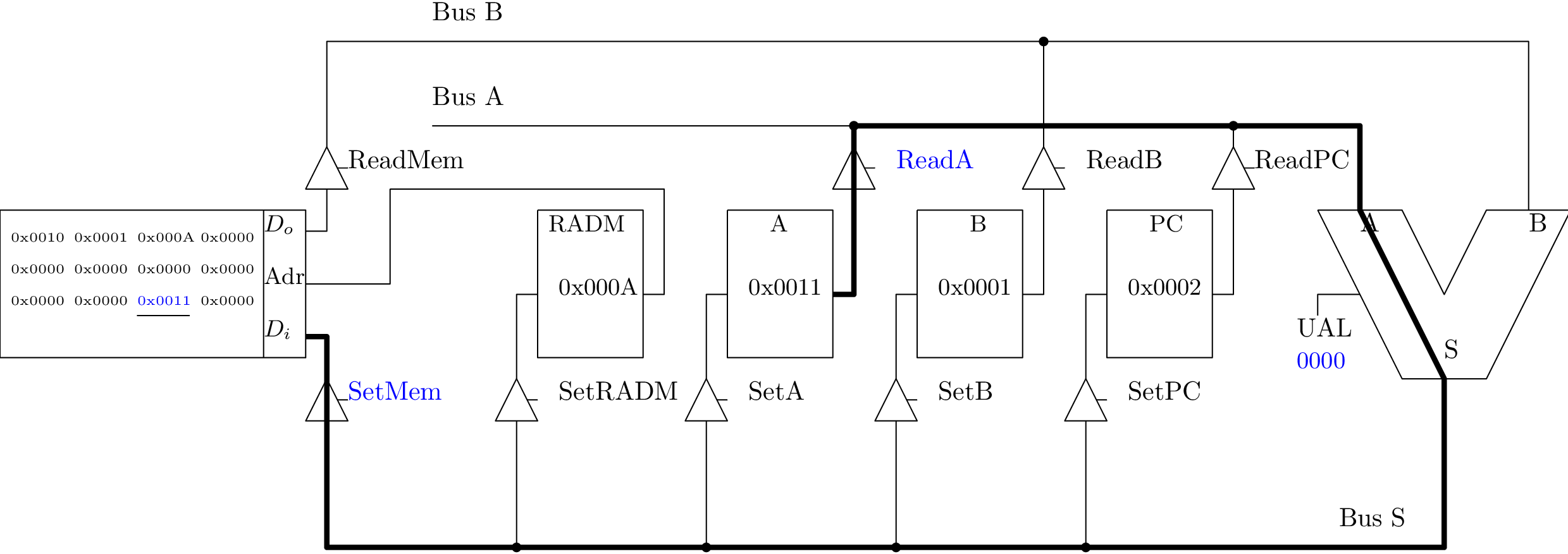
Chargement immédiat dans A (1/3)

Chargement A étape 1

Chargement immédiat dans A (2/3)

Chargement A étape 2

Chargement immédiat dans A (3/3)

Chargement A étape 3

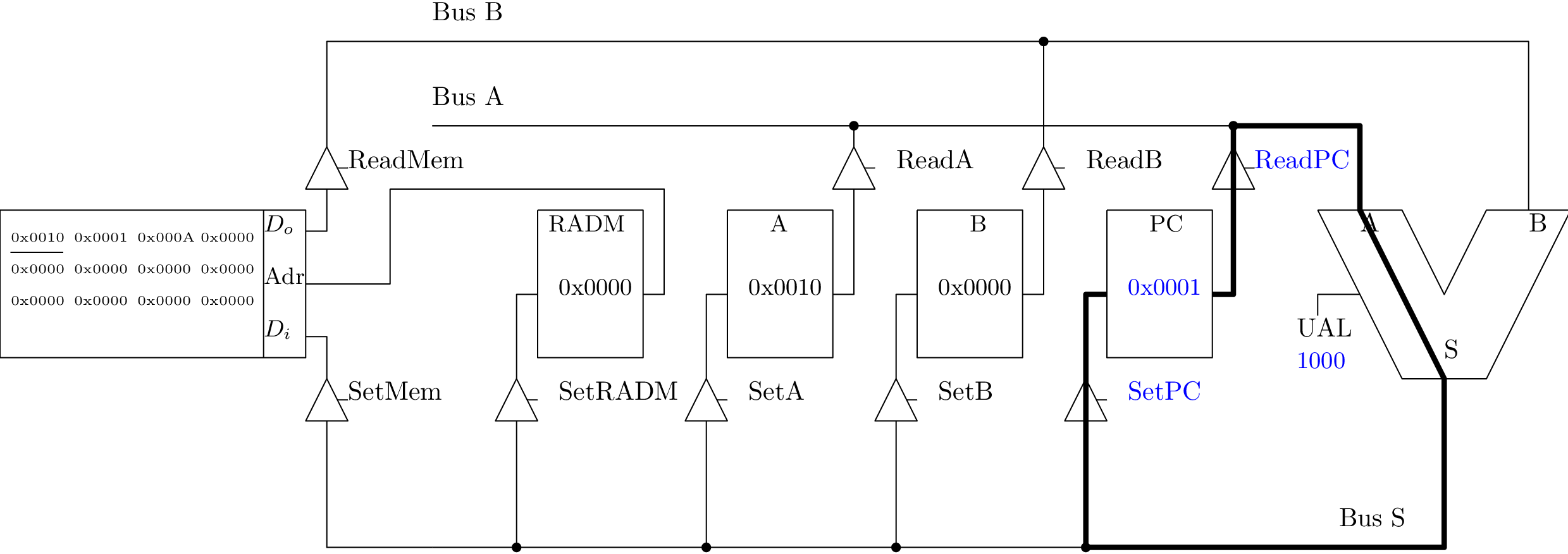
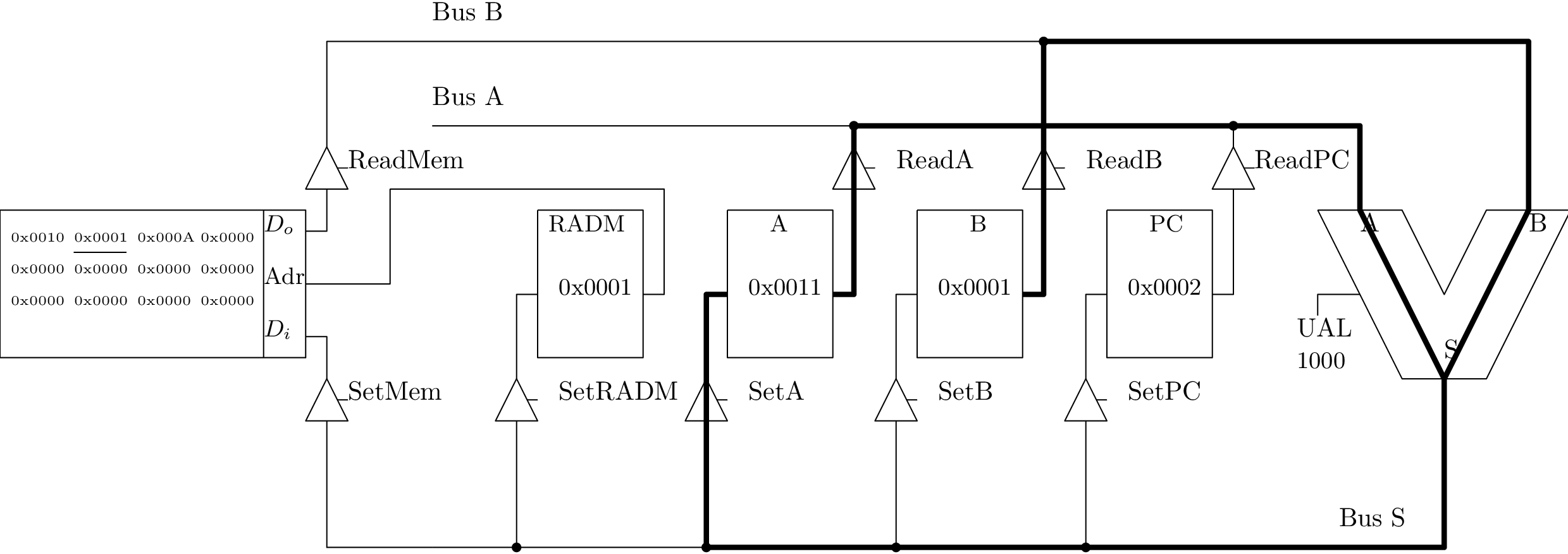
Chargement immédiat dans B (1/3)

Chargement B étape 1

Chargement immédiat dans B (2/3)

Chargement B étape 2

Chargement immédiat dans B (3/3)

Chargement B étape 3

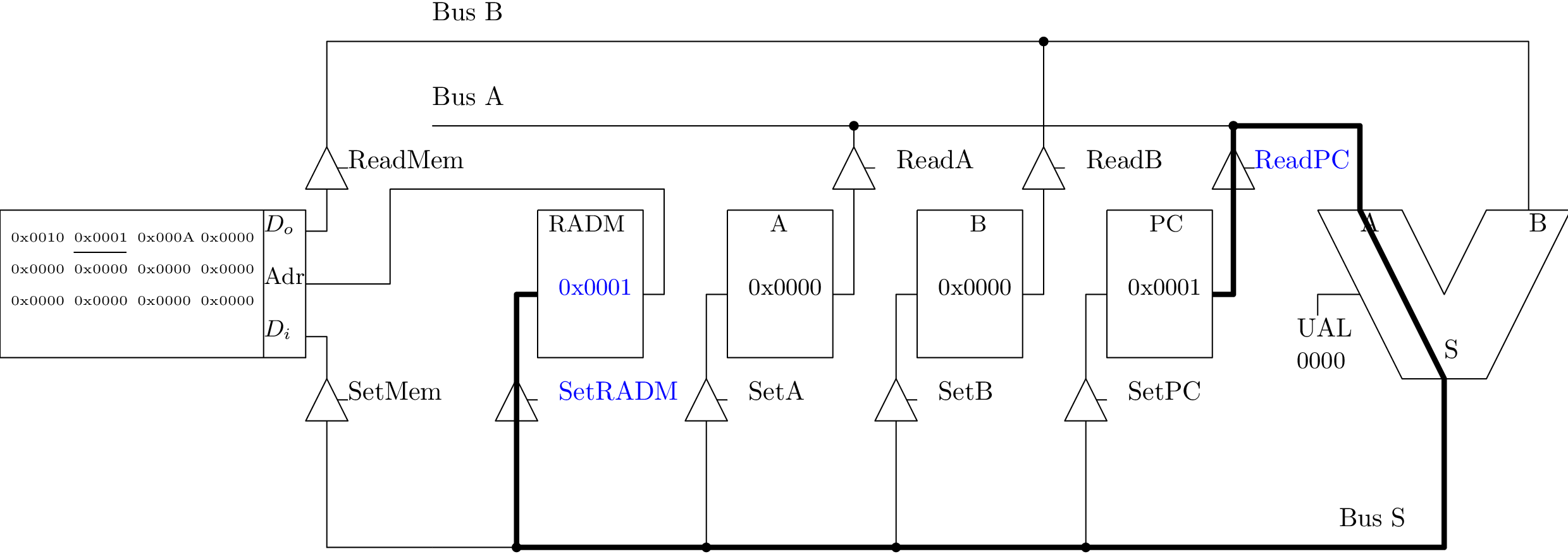
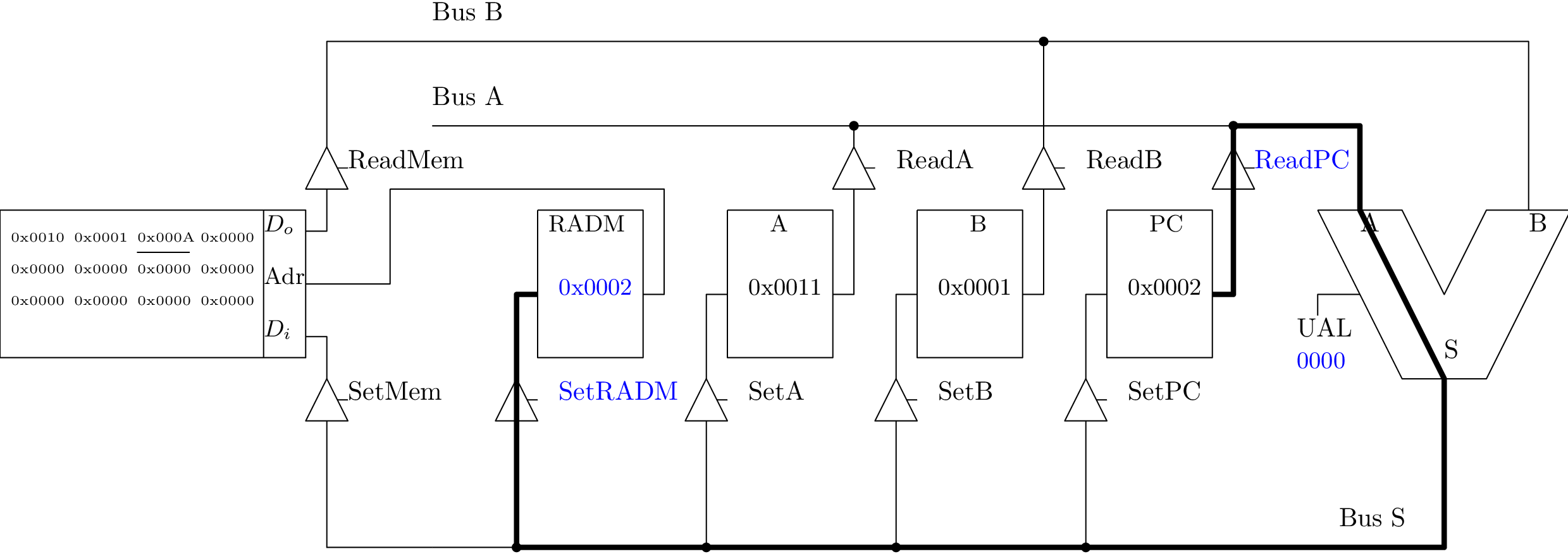
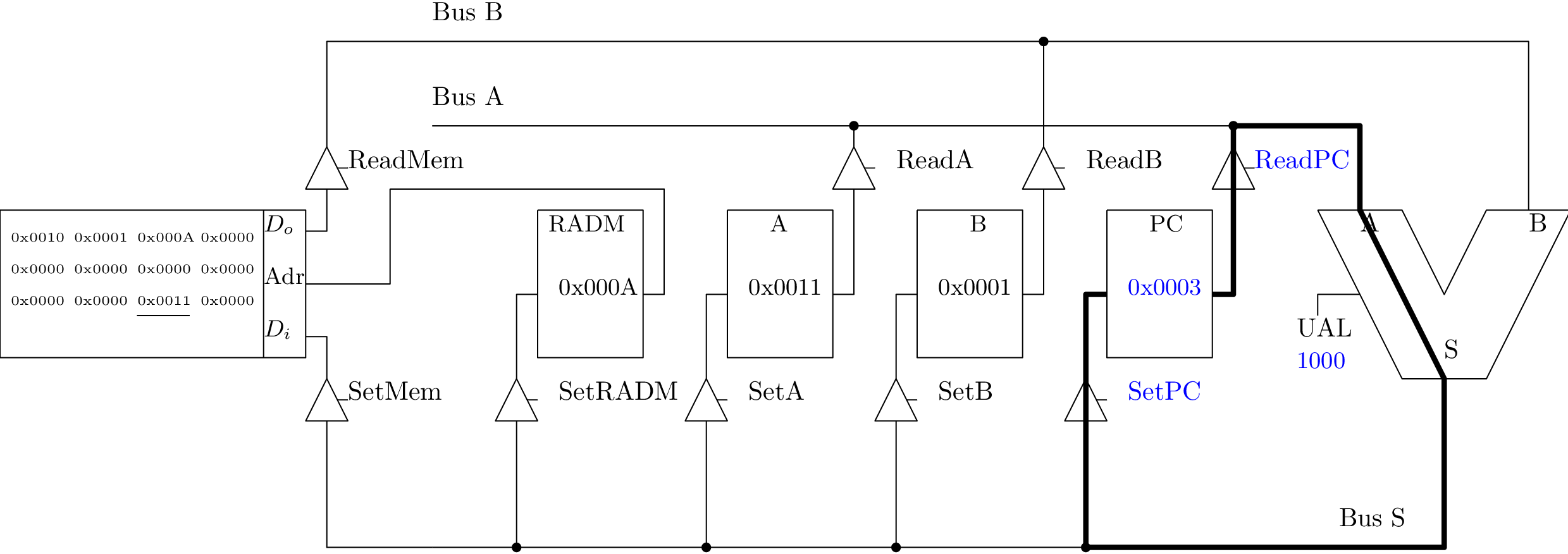
Addition : A := A + B

Addition A

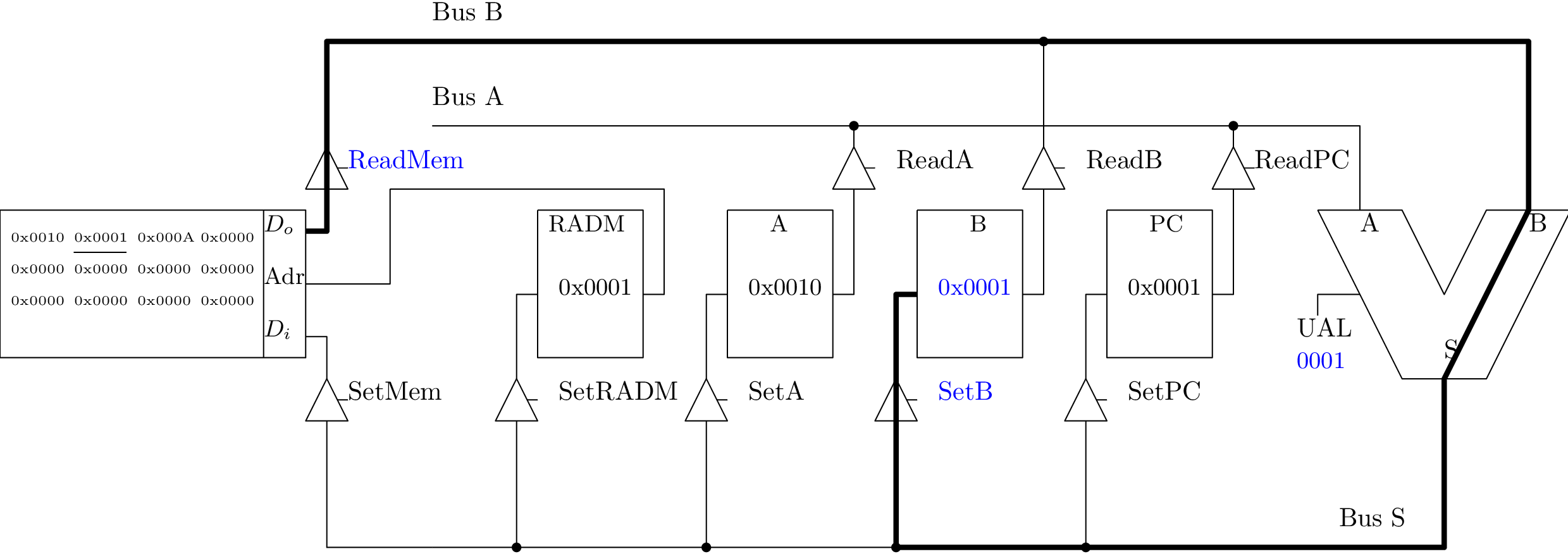
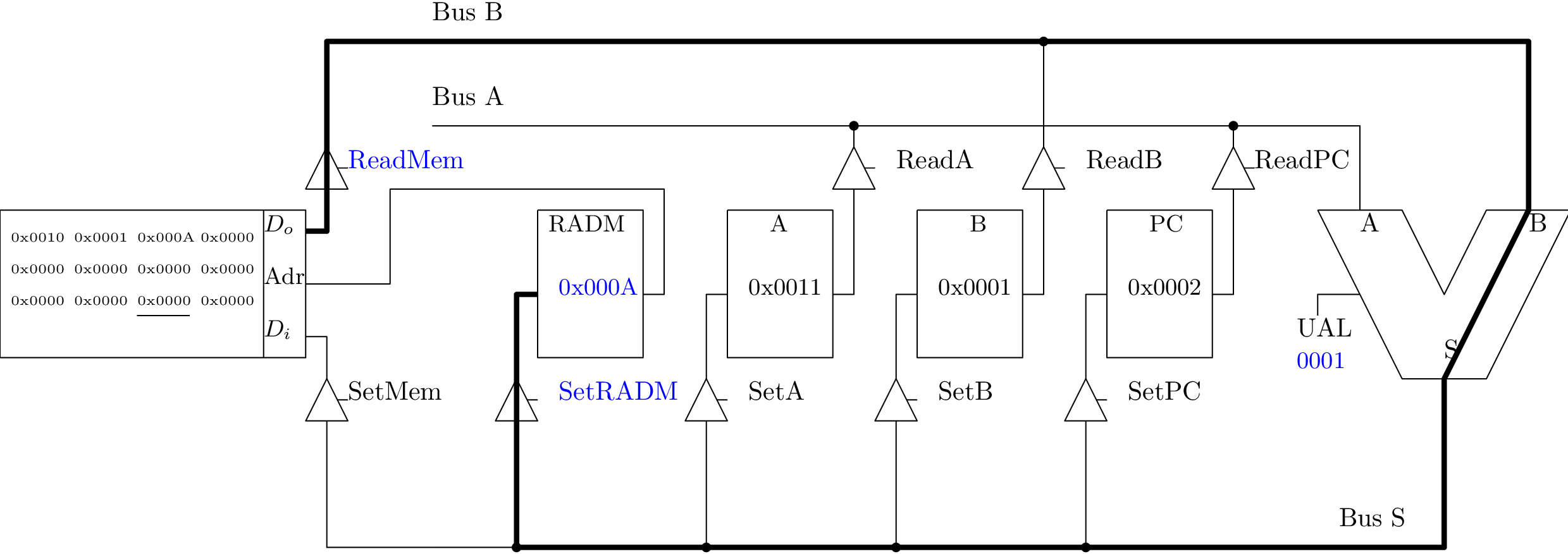
Sauvegarde du contenu du registre A en mémoire (1/4)

Sauvegarde A étape 1

Sauvegarde du contenu du registre A en mémoire (2/4)

Sauvegarde A étape 2

Sauvegarde du contenu du registre A en mémoire (3/4)

Sauvegarde A étape 3

Sauvegarde du contenu du registre A en mémoire (4/4)

Sauvegarde A étape 4

Modes d’adressage

• Adressage immédiat : le mot mémoire est la valeur à charger
• Adressage direct : le mot mémoire est l’adresse en mémoire de la valeur à charger, e.g. incrémenter un compteur dont la valeur courante est stockée à une adresse donnée en mémoire
• Adressage indirect : le mot mémoire est l’adresse à laquelle trouver l’adresse de la valeur à charger
• Adressage relatif : le mot mémoire contient l’adresse et un décalage, e.g. accéder aux éléments d’un tableau A[i]

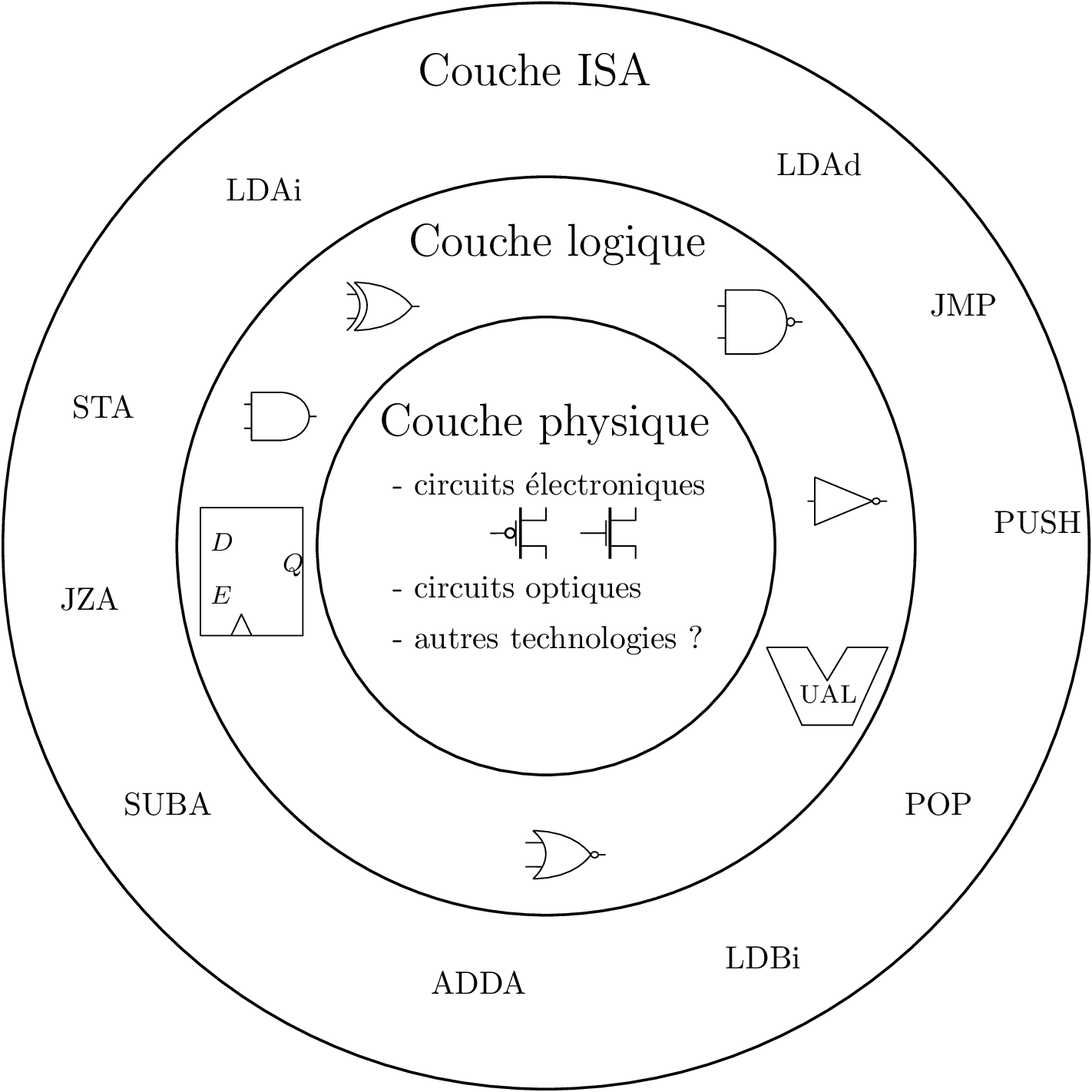
La couche ISA (Instruction Set Architecture)

La couche ISA

Couches architecture

Approche par couches d’abstractions successives

En plus des données, définissons le programme

Architecture de von Neumann : mémoire (data+prog) ↔︎ processeur

Les instructions

Adresses	Contenu
0000	0010	0001	000A	0000
0004	0000	0000	0000	0000
0008	0000	0000	0000	0000

Instructions en assembleur

Architecture de von Neumann : mémoire (data+prog) ↔︎ processeur

Les instructions

Adresses	Contenu
0000	LDAi	0010	LDBi	0001
0004	ADDA	STA	000A	0000
0008	0000	0000	0000	0000

Codage des instructions

Codage des instructions

Nom de l’instruction	Code de l’instruction
LDAi	0×1000
LDAd	0×1400
LDBi	0×2000
STA	0×1c00
ADDA	0×3000

Adresses	Contenu
0000	1000	0010	2000	0001
0004	3000	1c00	000A	0000
0008	0000	0000	0000	0000

⇒ Programme en langage machine

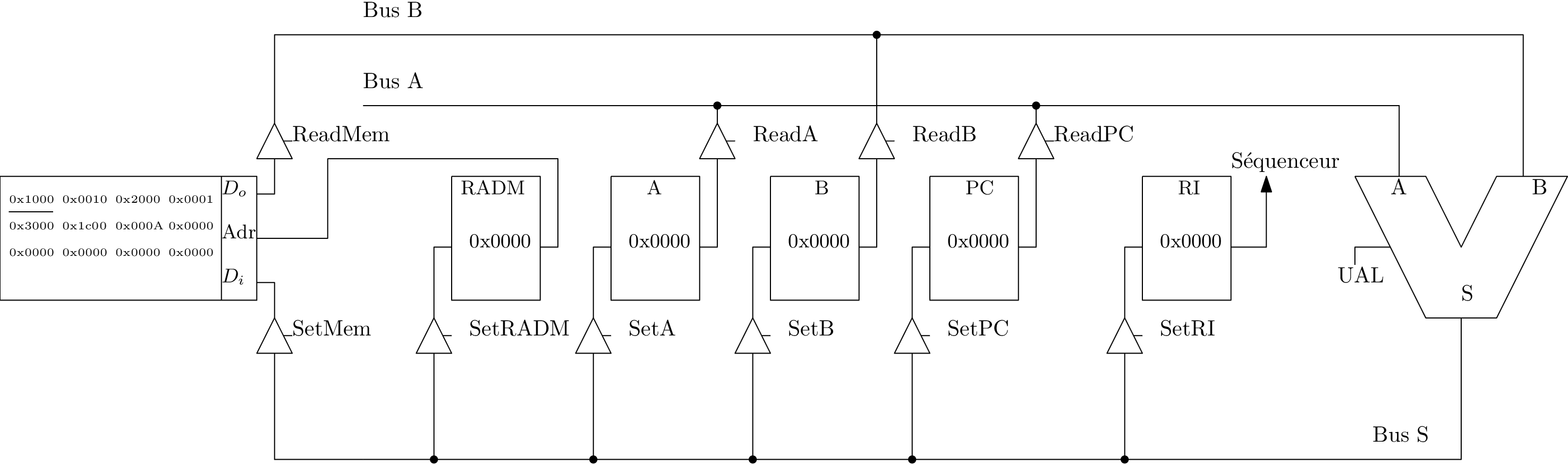
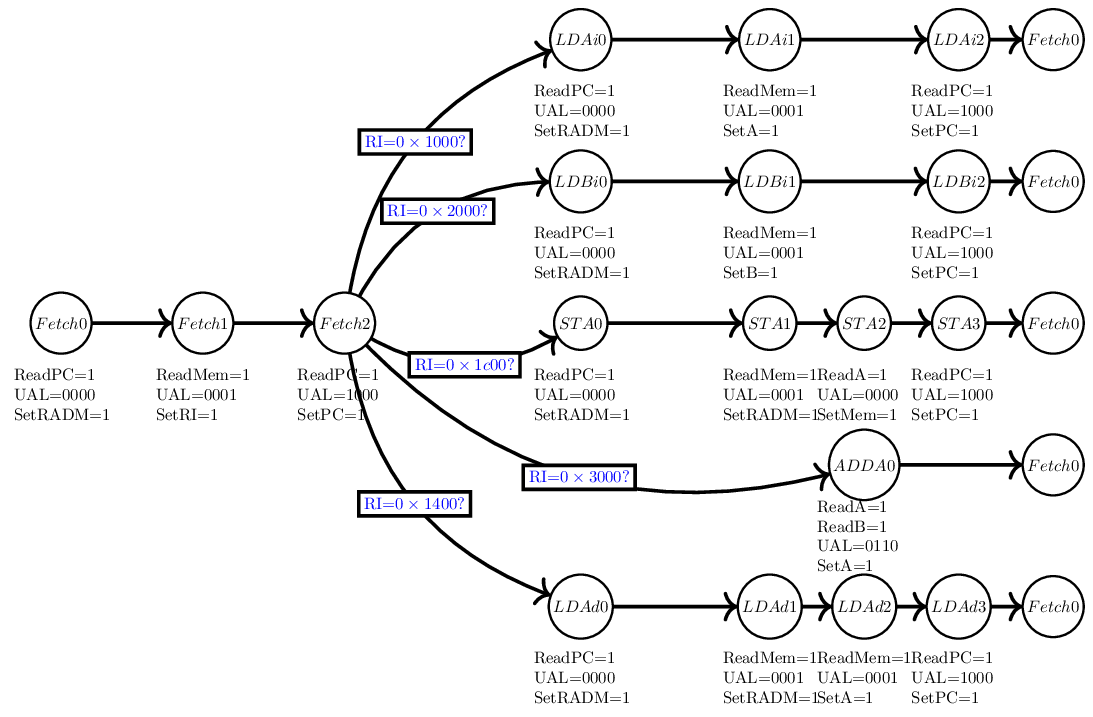
Récupérer l’instruction (fetch)

Une première possibilité avec un registre dédié

Premier chemin RI

L’instruction est :

• récupérée en mémoire
• placée dans le registre d’instruction (RI)
• qui est une entrée du séquenceur

Séquencement du chemin de données

Séquenceur

Séquence de signaux de contrôle spécifique :

1. pour récupérer l’instruction fetch
2. en fonction de l’instruction, pour la réaliser

⇒ machine à états finis qui génère les micro-instructions et dont l’état est stocké dans un registre dédidé microPC

Générer les signaux de contrôle : le séquenceur

Fetch

Premier chemin RI

FSM Fetch

Chargement immédiat dans A : LDAi

Premier chemin RI

FSM LDAi

Chargement immédiat dans B : LDBi

Premier chemin RI

FSM LDBi

Chargement direct dans A : LDAd

Premier chemin RI

FSM LDAd

Addition A:= A + B : ADDA

Premier chemin RI

FSM ADDA

Sauvegarde de A en mémoire : STA

Premier chemin RI

FSM STA

Machine à états finis pour le séquenceur

FSM complète

Réalisation matérielle ? Soyons astucieux sur le codage des états en codant les instructions à partir de l’adresse définie par les 8 bits de poids forts.

Séquenceur micro-programmé

Séquenceur micro

Notre première architecture interne

En ajoutant le séquenceur

Premier chemin séquenceur

Les micro-instructions

Séquenceur micro

• ROM[0x00] : saut à fetch
• ROM[0x08,0x09,0x0A,0x0B] : fetch/decode
• ROM[0x10,0x11,0x12,0x13] : LDAi
• ROM[0x14,0x15,0x16,0x17] : LDAd
• ROM[0x1c,0x1d,0x1e,0x1f] : LDAd
• ROM[0x20,0x21,0x22,0x23] : LDBi
• ROM[0x30,0x31,0x32,0x33] : ADDA

Les branchements

\[fact(n) = \begin{cases} \text{si } n=0 \text{ alors}& 1\\ \text{sinon }& n \times fact(n-1) \end{cases}\]

si … alors … sinon ? Indicateurs de l’UAL

Instructions de branchement

• JMP (0×7000) \[\texttt{JMP op} \Leftrightarrow PC := op\]

• JZA (0×7400) \[\texttt{JZA op} \Leftrightarrow \begin{cases} PC := op & \text{si } A==0\\ PC := PC+1 & \text{sinon} \end{cases}\]

• JZB (0×7800) \[\texttt{JZB op} \Leftrightarrow \begin{cases} PC := op & \text{si } B==0\\ PC := PC+1 & \text{sinon} \end{cases}\]

Architecture avec branchement

Premier chemin séquenceur JMP

Table de vérité du branchement

Premier chemin séquenceur JMP

CodeMCount	Z	\(S_1S_0\)	Sémantique
000	0 ou 1	00	MicroPC := MicroPC+1
001	0 ou 1	01	MicroPC := @Adr
010	0 ou 1	10	MicroPC := Instruction
011	0	00	MicroPC := MicroPC+1 si la sortie de l’UAL ≠ 0
011	1	01	MicroPC := @Adr si la sortie de l’UAL == 0

La suite

Prochaines étapes

Dans les prochains slides, nous verrons :

• Procédures, pile et pointeur de pile
• Traduction, compilation, interprétation
  
• Les mémoires
• Les périphériques
• Les interruptions
• Suppléments