Architecture des ordinateurs
Procédures, pile et langages de haut niveau
CentraleSupélec
2025-11-23
Petite synthèse
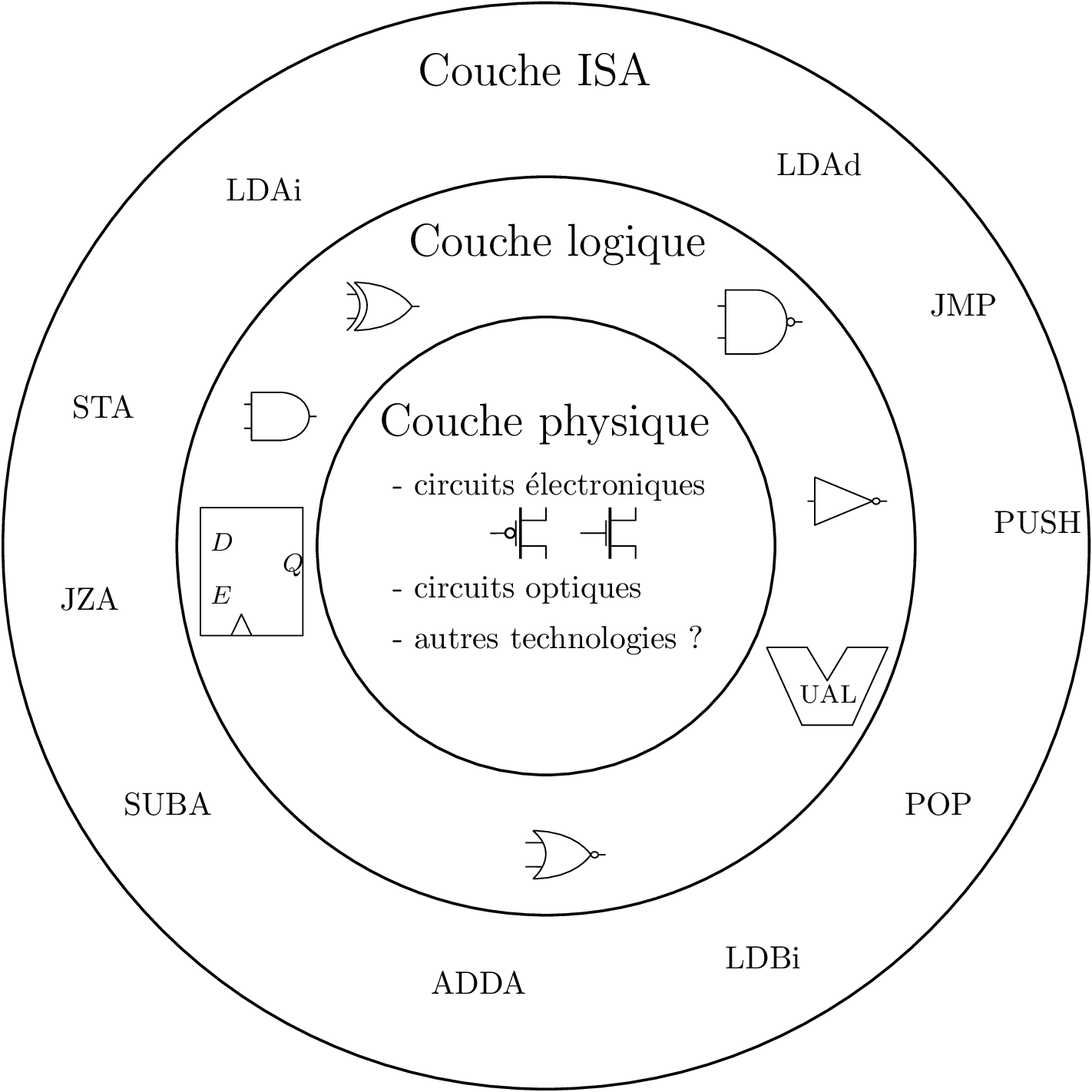
Petit retour sur l’architecture v0
Architecture à Jeu d’instructions (ISA)
| Code | Nom | Mots | Description |
|---|---|---|---|
| 0x0c00 | END | 1 | Fin du programme |
| 0x1000 | LDAi | 2 | Charge la valeur de l’opérande dans le registre A. [A:=opérande] |
| 0x1400 | LDAd | 2 | Charge la valeur dans la RAM pointée par l’opérande dans le registre A. [A:=Mem[opérande]]. |
| 0x1c00 | STA | 2 | Sauvegarde en mémoire la valeur du registre A à l’adresse donnée par l’opérande. [Mem[opérande]:= A] |
| 0x2000 | LDBi | 2 | Charge la valeur de l’opérande dans le registre B. [B:=opérande] |
| 0x2400 | LDBd | 2 | Charge la valeur dans la RAM pointée par l’opérande dans le registre B. [B:=Mem[opérande]]. |
| 0x2c00 | STB | 2 | Sauvegarde en mémoire la valeur du registre B à l’adresse donnée par l’opérande. [Mem[opérande]:= B] |
| 0x3000 | ADDA | 1 | Ajoute le contenu des registres A et B et mémorise le résultat dans le registre A. [A:=A+B] |
| 0x3400 | ADDB | 1 | Ajoute le contenu des registres A et B et mémorise le résultat dans le registre B. [B:=A+B] |
| 0x3800 | SUBA | 1 | Soustrait le contenu des registres A et B et mémorise le résultat dans le registre A. [A:=A-B] |
| 0x3c00 | SUBB | 1 | Soustrait le contenu des registres A et B et mémorise le résultat dans le registre B. [B:=A-B] |
| 0x4000 | MULA | 1 | Multiplie le contenu des registres A et B et mémorise le résultat dans le registre A. [A:=AxB] |
| 0x4400 | MULB | 1 | Multiplie le contenu des registres A et B et mémorise le résultat dans le registre B. [B:=AxB] |
| 0x4800 | DIVA | 1 | Divise le contenu du registre A par deux et mémorise le résultat dans A. [A:=A/2] |
| 0x5000 | ANDA | 1 | Calcule un ET logique entre le contenu des registres A et B et mémorise le résultat dans A. [A:=A&B] |
| 0x5400 | ANDB | 1 | Calcule un ET logique entre le contenu des registres A et B et mémorise le résultat dans B. [B:=A&B] |
| 0x5800 | ORA | 1 | Calcule un OU logique entre le contenu des registres A et B et mémorise le résultat dans A. [A:=A|B] |
| 0x5c00 | ORB | 1 | Calcule un OU logique entre le contenu des registres A et B et mémorise le résultat dans B. [B:=A|B] |
| 0x6000 | NOTA | 1 | Mémorise dans A la négation de A. [A:=!A] |
| 0x6400 | NOTB | 1 | Mémorise dans B la négation de B. [B:=!B] |
| 0x7000 | JMP | 2 | Saute inconditionnellement à l’adresse donnée par l’opérande. [PC:=operande] |
| 0x7400 | JZA | 2 | Saute à l’adresse donnée par l’opérande si le contenu du registre A est nul. [PC:=operande si A=0] |
| 0x7800 | JZB | 2 | Saute à l’adresse donnée par l’opérande si le contenu du registre B est nul. [PC := operande si B=0] |
Automate à états finis du séquenceur
Séquenceur et programme
Séquenceur
- Sémantique des instructions
- Générique
- Automate à états finis : état dans MicroPC, signaux de contrôle ROM[MicroPC]
Programme
- Qu’est ce que je veux calculer ?
- Spécifique
- Séquence de codes d’instructions et de données en RAM
Aperçu de quelques architectures
La notre
- 2 registres banalisés : A et B
- 2 registres internes : RADM et PC
- adresses sur 16 bits, données sur 16 bits
- Format des instructions : \(1\) mot de \(16\) bit pour l’instruction, \(1\) mot pour l’opérande éventuelle
- jeu d’instructions : LDAi, LDBi, ADDA, ANDB, JMP, JZA
- horloge maximale sous logisim : 4 kHz
Beaucoup d’architectures :
https://en.wikipedia.org/wiki/List_of_instruction_sets
Intel x86 IA32-64
Du Intel 8086(1978) jusqu’au Intel Core i7 (2015)
Note
- 4 registres banalisés 32 bits EAX, EBX, ECX, EDX,
- 4 registres d’index : ESI, EDI, EBP (Base pointer), ESP (Stack pointer)
- 6 registres de segments 16 bits : CS, DS, SS,ES, FS, GS
- 1 registre de status 32 bits : EFLAGS
- x registres internes : EIP (Instruction Pointer == PC) (32 bits)
Intel 64 and IA-32 Architectures Software Developer Manuals
https://software.intel.com/en-us/articles/intel-sdm
Intel x86 IA32-64
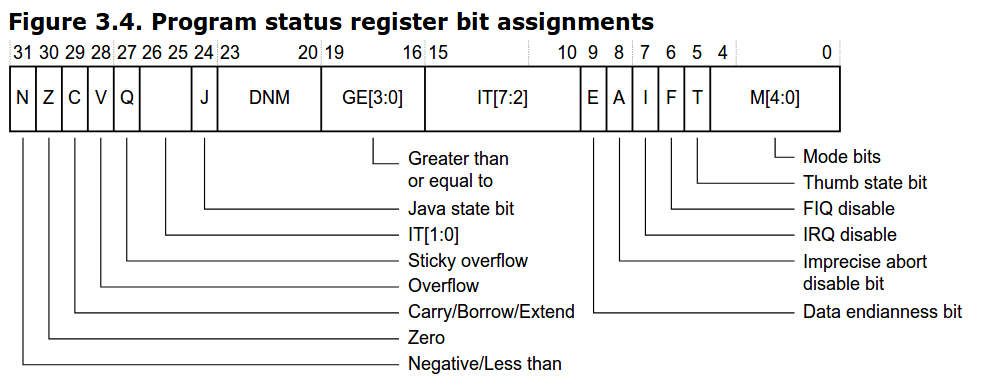
Carry Flag (CF), Sign Flag (SF), Zero Flag (ZF),
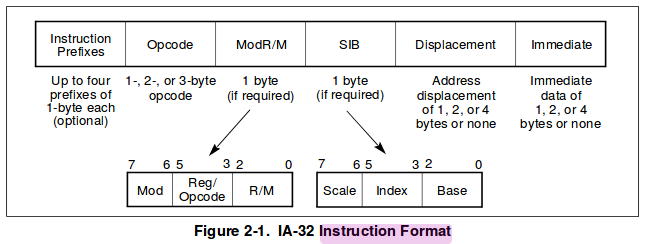
Intel x86 IA32-64
Beaucoup d’instructions : 1.300 mnémoniques, plusieurs modes d’adressages, ..
Documentation des instructions https://cdrdv2.intel.com/v1/dl/getContent/671110.
ARM (téléphones, tablettes, consoles)
Acorn RISC Machine architecture (1980) jusqu’au ARMv8.3-A (2016)
Note
- 16 registres \(R_i\) 32 bits dont :
- \(R_0-R_3\) : arguments/résultats pour une routine
- \(R_4-R_8\) : variables temporaires
- \(R_9\) : Plateform register
- \(R_{10}\) : Stack limit pointer
- \(R_{11}\) : Frame pointer
- \(R_{12}\) : registre temporaire
- \(R_{13}\) : Stack Pointer
- \(R_{14}\) : Link register (adresse de retour)
- \(R_{15}\) : Programm Counter
- 1 registre de statut CPSR 32 bits
http://infocenter.arm.com/help/index.jsp
Voir l’intervention de ST Micro.
ARM (téléphones, tablettes, consoles)
ARM - Jeu d’instructions
La v0 est conçue, programmons la !
Chemin de données et programmation
C’est dur et long pour le moment de programmer
Calculer la suite de Syracuse
\[\forall n \in \mathbb{N}^*, u_{n+1} = \begin{cases} u_n/2 & \mbox{si } u_n \mbox{ est pair}\\ 3u_{n+1}+1 & \mbox{ sinon} \end{cases}\] \[u_0 = 127 ; u_{n} = ?\]
⇔
Code machine
1000 007f 1c00 0024 1c00 1000 1400 0024 2000 0001 5000 7400 001b 1400 0024 2000 0003 4000 2000 0001 3000 1c00 0024 1c00 1000 7000 0006 1400 0024 4800 1c00 0024 1c00 1000 7000 0006
si si, je vous assure. Donc, c’est dur et long.
C’est dur et long pour le moment de programmer
Calculer la suite de Syracuse
\[\forall n \in \mathbb{N}^*, u_{n+1} = \begin{cases} u_n/2 & \mbox{si } u_n \mbox{ est pair}\\ 3u_{n+1}+1 & \mbox{ sinon} \end{cases}\] \[u_0 = 127 ; u_{n} = ?\]
⇔
Code machine
[LDAi 007f STA 0024 STA 1000] [LDAd 0024 LDBi 0001 ANDA JZA 001b] [LDAd 0024 LDBi 0003 MULA LDBi 0001 ADDA STA 0024 STA 1000 JMP 0006] [LDAd 0024 DIVA STA 0024 STA 1000 JMP 0006]
Comment faire pour simplifier la programmation ?
Les procédures (ou fonctions)
Définition : succession d’opérations à exécuter pour accomplir une tâche déterminée [Larousse]
Exemple de Syracuse en Python:
Les procédures : illustration
- programme de \(f\) : \(0\times 0014\)
- on utilise ici explicitement le registre A pour stocker les arguments et le résultat
- retour ?
Implémenter les procédures
Nous avons donc \(4\) problèmes à résoudre :
- comment partir exécuter la routine ? JMP
- comment passer les arguments à la routine ?
- Registres dédiés : combien ?? (e.g. \(R_0-R_3\) pour ARM)
- autre chose ?
- comment revenir au programme appelant ?
- sauvegarder l’adresse de retour dans un registre dédié : link register à sauvegarder lors d’appels cascadés (A appelle B qui appelle C qui appelle …), e.g. ARM
- autre chose ?
- comment récupérer le résultat ?
- un registre dédié ? (e.g. \(R_0\) pour ARM)
- autre chose ?
Dans notre architecture, on va répondre à ces \(3\) dernières questions en utilisant une structure particulière : la pile
Procédures, pile et pointeur de pile
Procédures, pile et pointeur de pile
Spécifications d’une pile
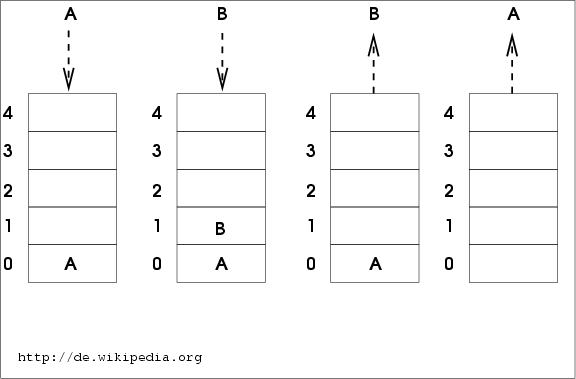
Une pile en mémoire
- structure de données en mémoire principale (RAM)
- empiler, dépiler une valeur : sommet de pile
- ou est le sommet de pile : registre Stack Pointer
- le sommet de la pile désigne la prochaine zone mémoire libre
Ajout de SP dans le chemin de données
Ajout d’instructions de manipulation de la pile
Spécifications
- ou placer la pile en mémoire ?
- quelle est l’adresse du sommet de la pile en mémoire ?
- comment empiler/dépiler, écrire/lire des éléments de la pile ?
Instructions particulières
- pour manipuler le registre SP : LDSPi, STSP, INCSP, DECSP
- pour empiler/dépile : PUSH{A,B}, POP{A, B}
- pour lire/écrire relativement à SP : POKE{A,B}, PEEK{A,B}
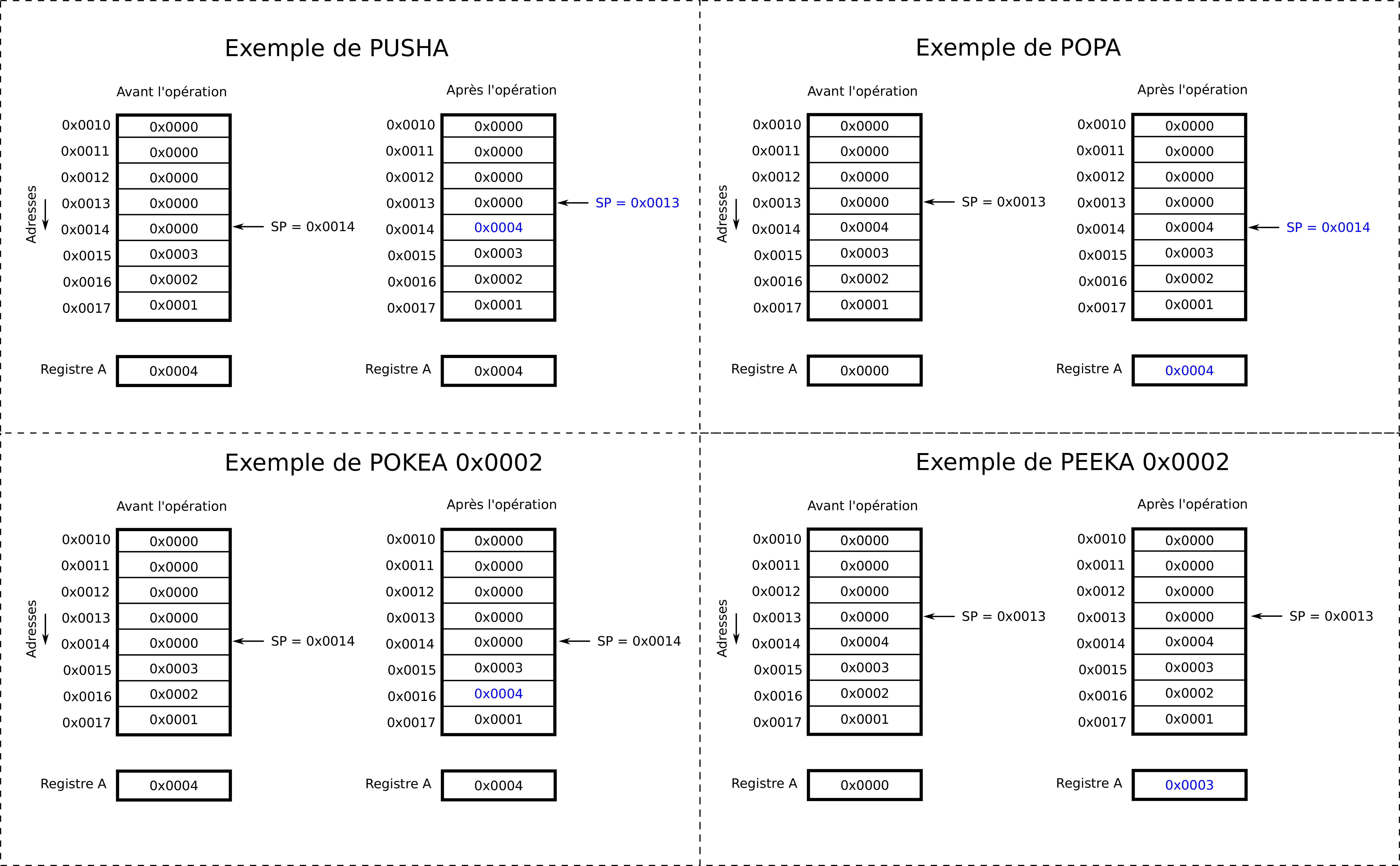
PUSH, POP, POKE, PEEK, Hum?!
→ Machines à états (b0, b4, b8, bc)?
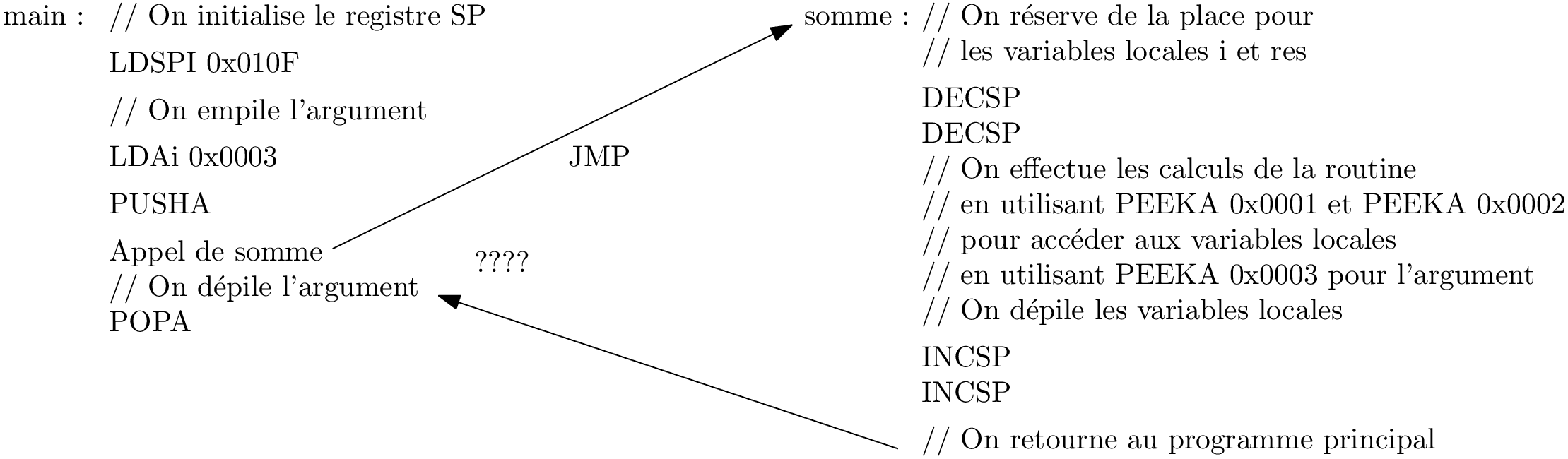
Utilisons la pile pour passer des arguments
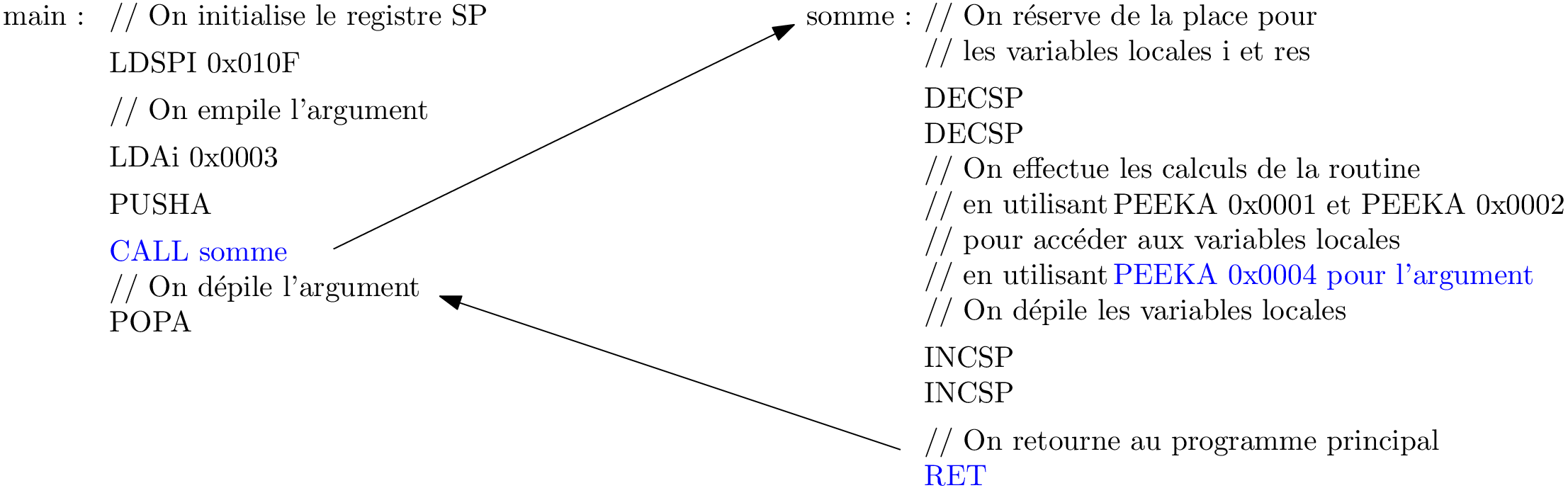
Somme: Une première tentative, juste JMP ?
Appel et retour de routines
Spécifications
- Quand on part exécuter le code d’une procédure, il faut sauvegarder là où retourner (marque page)
- Quand on termine une procédure, il faut poursuivre le programme appelant
Instructions particulières
- CALL (0xA000): “CALL op” Empile l’adresse de la prochaine instruction et branche
- RET (0xA800): “RET” Dépile dans PC l’adresse de retour
Attention, il faut penser à l’ajout de l’adresse de retour lorsqu’on indexe la pile (e.g. PEEK, POKE).
Réalisation de ces instructions
Réalisation de ces instructions
Réalisation de ces instructions
et le résultat au fait? La pile !
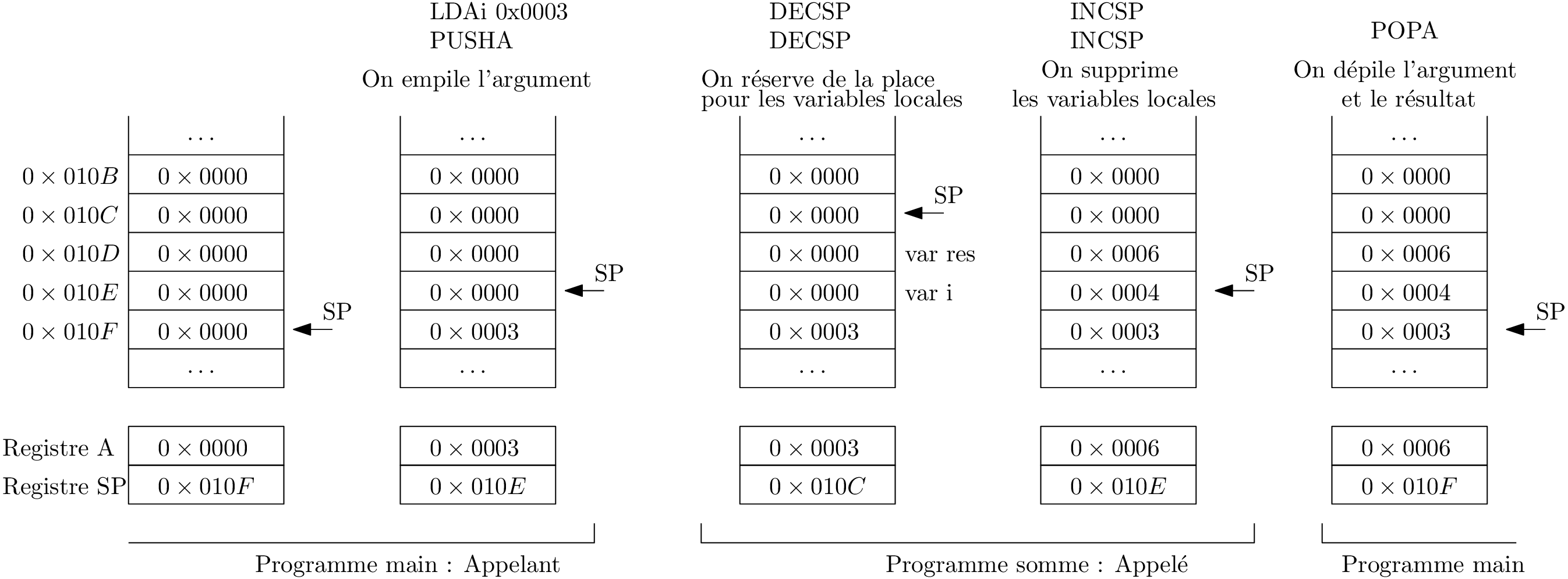
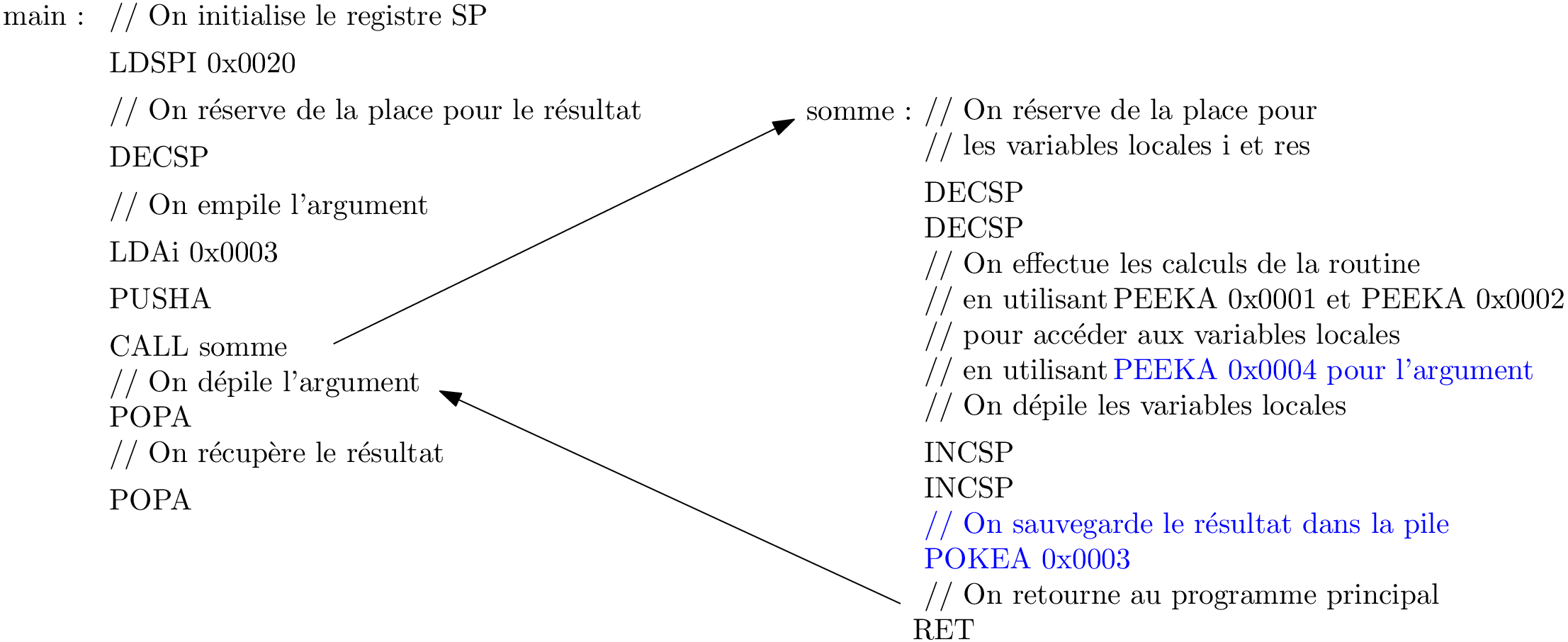
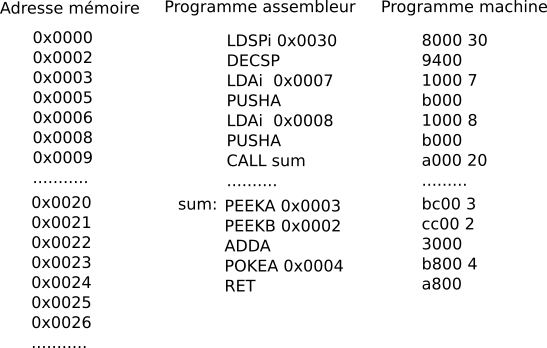
Somme : une deuxième tentative
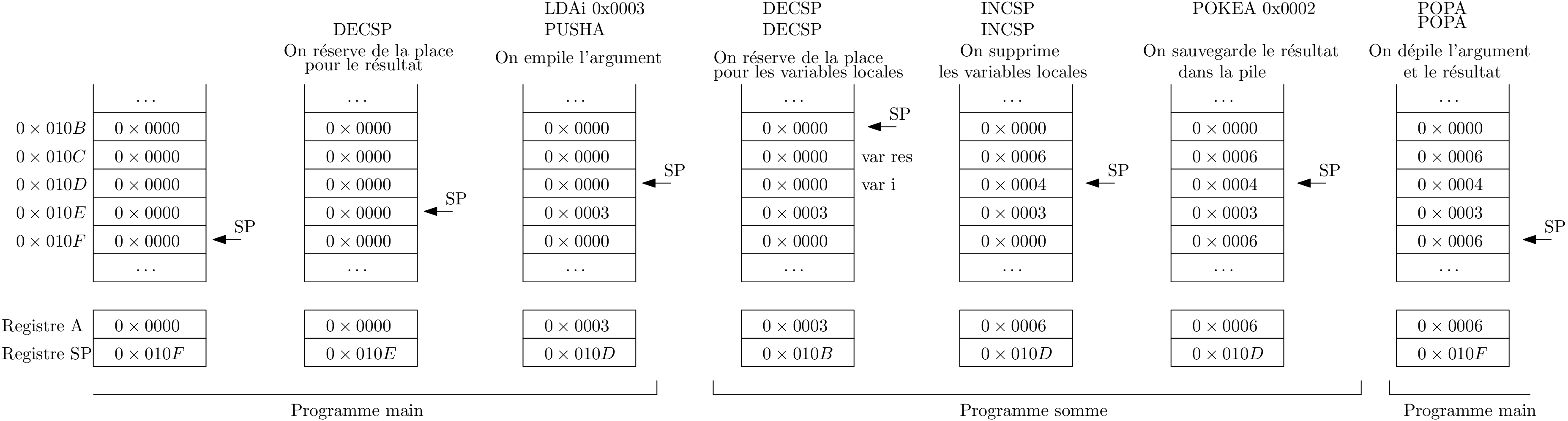
Déroulement d’un appel de routine
Le programme appelant
- réserve de la place pour le résultat (DECSP)
- empile les arguments (PUSH)
- sauvegarde la valeur PC après lecture de l’adresse de la routine et branche sur la routine (CALL)
Programme appelé
- lit les arguments dans la pile (PEEK),
- calcule son résultat éventuel et le sauvegarde dans la pile (POKE)
- retourne au programme appelant (RET) : le registre SP doit être restauré!
Programme appelant
- dépile les arguments (INCSP ou POP)
- dépile le résultat (POP) et se poursuit
Qui met/enlève quoi dans la pile ?
Attention!
Dans cette version d’architecture, les accès PEEK, POKE sont relatifs au sommet de pile !
Autre possibilité : registre Base Pointer (BP) / Frame Pointer (FP)
Pour restaurer le registre SP, on pourrait aussi utiliser BP/FP
C’est parti pour le code machine de :
Les procédures permettent
- de factoriser le code
- d’éviter des bugs puisqu’on ne réécrit pas plusieurs fois le “même” code
- de rendre le code plus compact
mais avec un petit surcoût à l’exécution (parfois inévitable)
La pile permet
- de passer des arguments à une procédure
- de récupérer le résultat d’une procédure
- de sauvegarder l’adresse de retour d’une procédure
- de sauvegarder des variables locales à la procédure
Des fonctions récursives : Hanoï
Problème
Calculer le nombre de déplacement minimum nécessaires : \[h(n) = \begin{cases} 1 & \mbox{si } n=1 \\ 2h(n-1) + 1 & \mbox{sinon} \end{cases}\] \(h(4) = ?\)
Exercice : Définir le code assembleur pour calculer \(h(4)\).
Exécutons (à 8 Hz) et regardons le contenu de la pile pour visualiser les contextes.
Des fonctions récursives : Hanoï
La pile pourrait “déborder” \(\rightarrow StackOverflow\)
Au fait ..
Comment passer de la formalisation du problème à un algorithme efficace permettant de le résoudre ??
Cours SDA (1A - S06): Structures de Données et Algorithmes
Cours C++ (1A - S06): Programmation C++, structures de données, etc…
Cours Génie logiciel (2A - S07): Etude des méthodes et bonnes pratiques pour le développement logiciel
Simplifions la programmation de la machine
Souhaits
- un programme moins long, moins répétitif, moins sujet aux bugs : procédures et pile
- mais on programme toujours en code machine ?!?!
8000 0FFF
1000 0001
2000 0002
⋮
LDSPi 0x0FFF
LDAi 0x0001
LDBi 0x0002
⋮
La couche d’assemblage
La couche d’assemblage
Langage d’assemblage et assembleur
Assembleur : programme traduisant langage d’assemblage → code machine.
Abus : programme assembleur = programme en langage d’assemblage
Quelques éléments de syntaxe de notre assembleur
Spécifications
- On utilise les mnémoniques LDAi, LDBi, STA, CALL, …
- les valeurs en hexadécimal sans préfixe 0x
- “;;” commentaire
- étiquettes : pour les branchements, pour les variables; spécial @stack@
- pseudo-instructions : e.g.
- DSW : allocation de variables globales; par convention en début de programme!
Les variables et les étiquettes ne doivent pas être interprétables en hexadécimal.
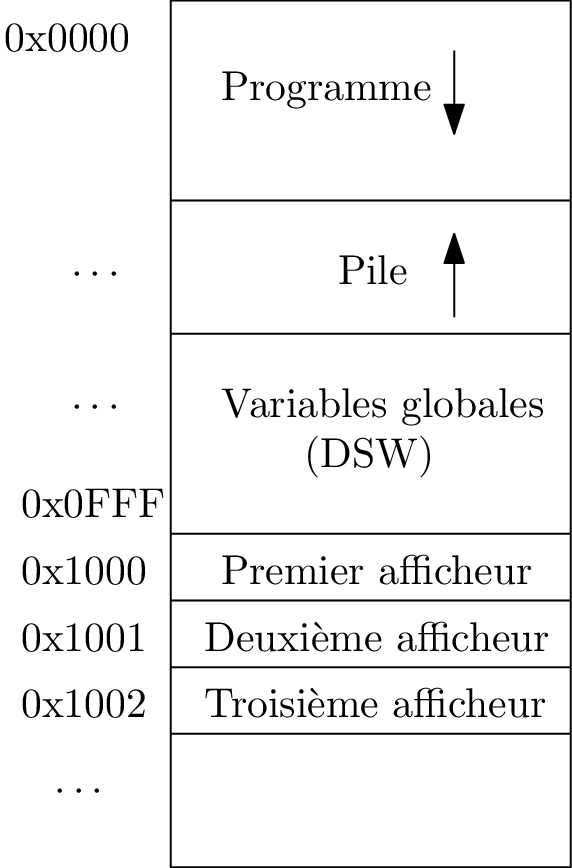
Disposition du programme et des données en mémoire (chez nous)
Traduction de quelques structures de contrôle
La boucle tant que
En pseudo-code
tant que i ≠ 0 faire
res ← res + i
i ← i - 1
fin tant queTraduction de quelques structures de contrôle
La boucle for est équivalente à la boucle tant que
for ⇔ while
pour (i = 0 ; i < N ; i = i + 1) faire
res ← res + i
fin pour⇔
i ← 0
tant que i < N faire
res ← res + i
i ← i + 1
fin tant quefor ⇔ while
pour (init; condition ; incrément) faire
action
fin pourinit
tant que condition faire
action
incrément
fin tant queTraduction de quelques structures de contrôle
Les tests conditionnels :
Pseudo-code
si x ≠ 0 alors
x ← 1
fin si
x ← x + 1Traduction de quelques structures de contrôle
Pseudo-code
si x == 10 alors
x ← 0
sinon
x ← x + 1
fin siL’assembleur : traduction en code machine
Exercice : Assembler le programme
u ← 127
tant que vrai faire
u ← next(u)
print(u)
fin tant que
fonction next(u)
si u pair alors
retourner u/2
sinon
retourner 3*u + 1
fin si
fin fonctionCompteur d’emplacement, table des symboles, variables globals; cf syr.asm
Démo : python assemble.py
Langages de haut niveau
Langage de haut niveau (Python, C, C++, Scala, ..)
Mais pourquoi ?
Assembleur
- spécifique à une architecture
- encore dur à programmer (
LDAd b; LDBd c; ADDA; STA a) - peu de vérification syntaxique: on peut ajouter des choux et des carottes
Langage de haut niveau
- indépendant de l’architecture
- langage plus intuitif, e.g. \(a = b + c\), structures de contrôle, définition de fonctions
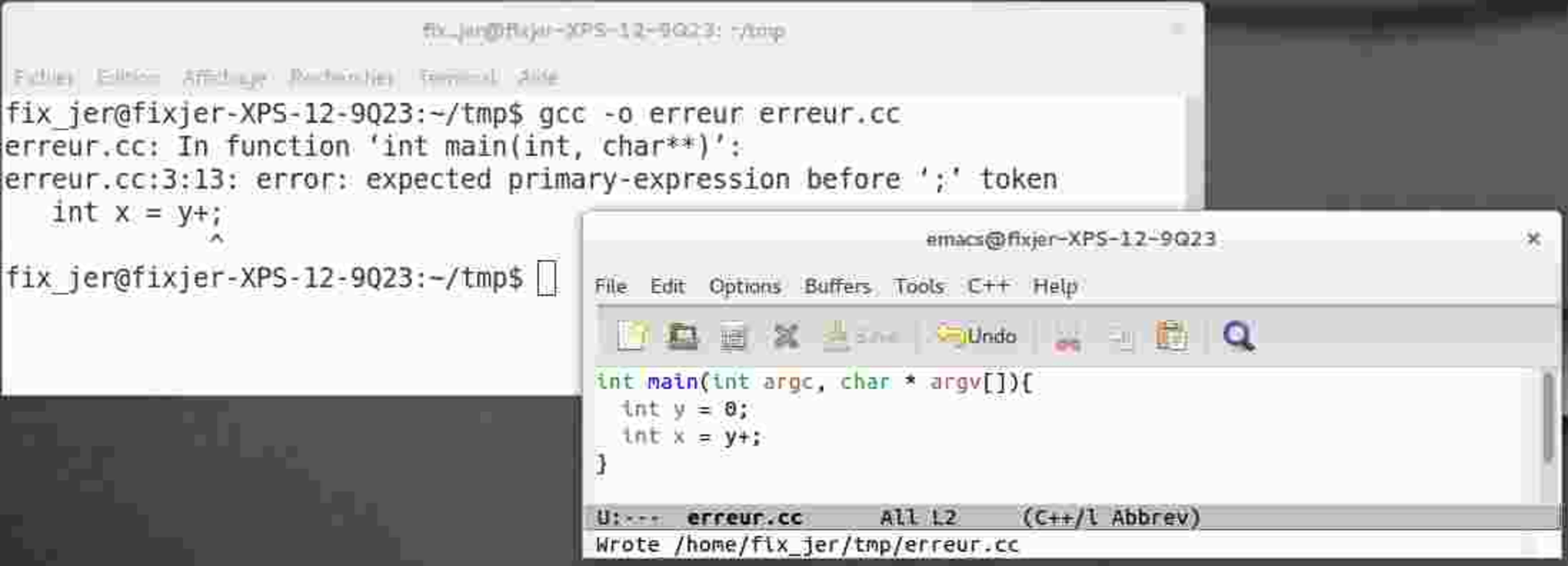
- vérification syntaxique
Langage : Interprété ou compilé
Langage interprété
Un programme (interpréteur) interprète “à la volée” le code source
Ex : Python/ python
python main.py
⇒ Machine virtuelle python
Brève Anatomie d’un compilateur
Références :
- “The dragon book” Aho, Lam, Sethi, Ullman
- “Modern Compiler Implementation”, A. Appel
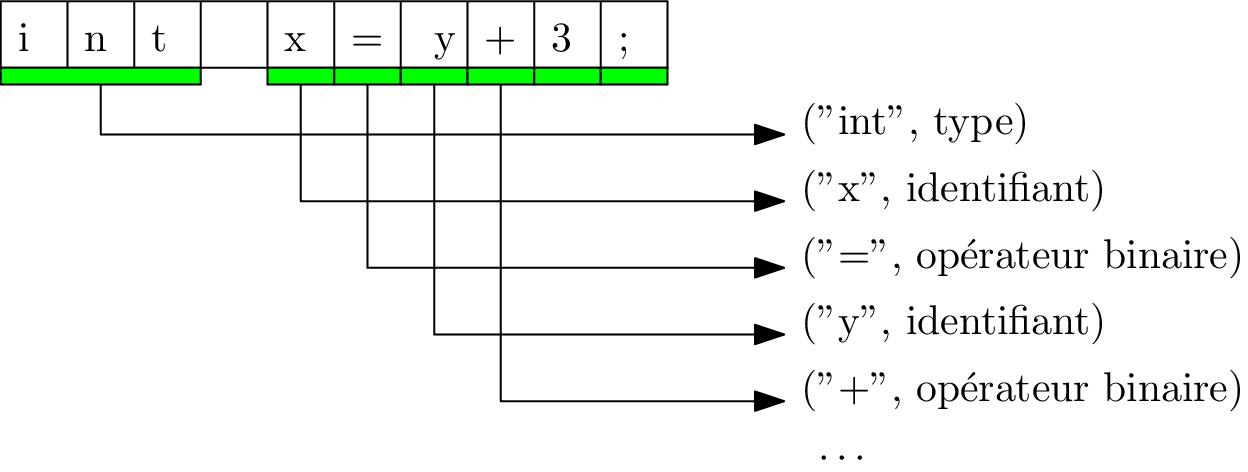
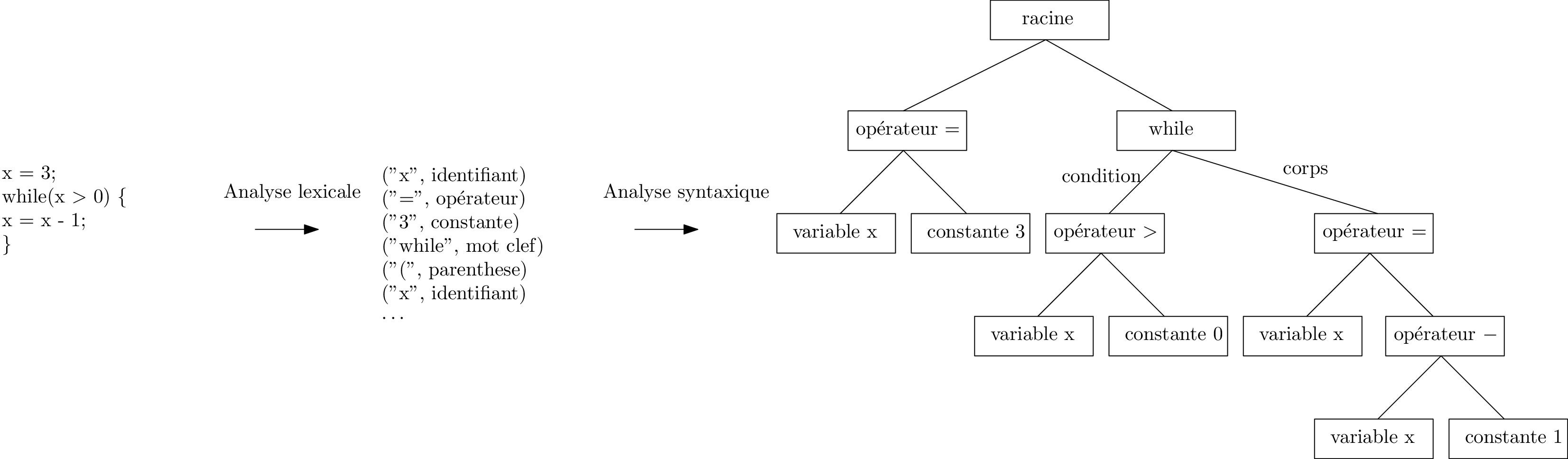
La phase d’analyse (frontend)
La phase d’analyse (frontend)
Génération et optimisation d’une représentation intermédiaire
Représentation intermédiaire
- indépendante du langage source (C, C++, ..) et de l’architecture (x86, ARM, CentraleSupelec)
- facile à produire, facile à convertir en code machine
- optimisable
Ex : register transfer language, gimple, generic, three adress code, single static assignment, control flow graph, …
Example de représentation : Three Address Code
- opérations binaires :
x := y op z - opérations unaires :
x:= op y - copies :
x := y - sauts (in)conditionnels :
goto L;If x relop y goto L - procédures :
param x1,..call p,return y - …
Références :
- “The dragon book” Aho, Lam, Sethi, Ullman
- “Modern Compiler Implementation”, A. Appel
Exemple de représentation intermédiaire : Three Adress code
En C++ :
Représentation 3-Address Code
x = 3;
_t1 = 2 + 7;
y = _t1 + x;
z = 2 * y;
_t2 = x < y;
IfZ _t2 Goto _L0;
_t3 = x / 2;
_t4 = y / 3;
z = _t3 + _t4
Goto _L1
_L0: _t5 = x * y;
z = _t5 + z;
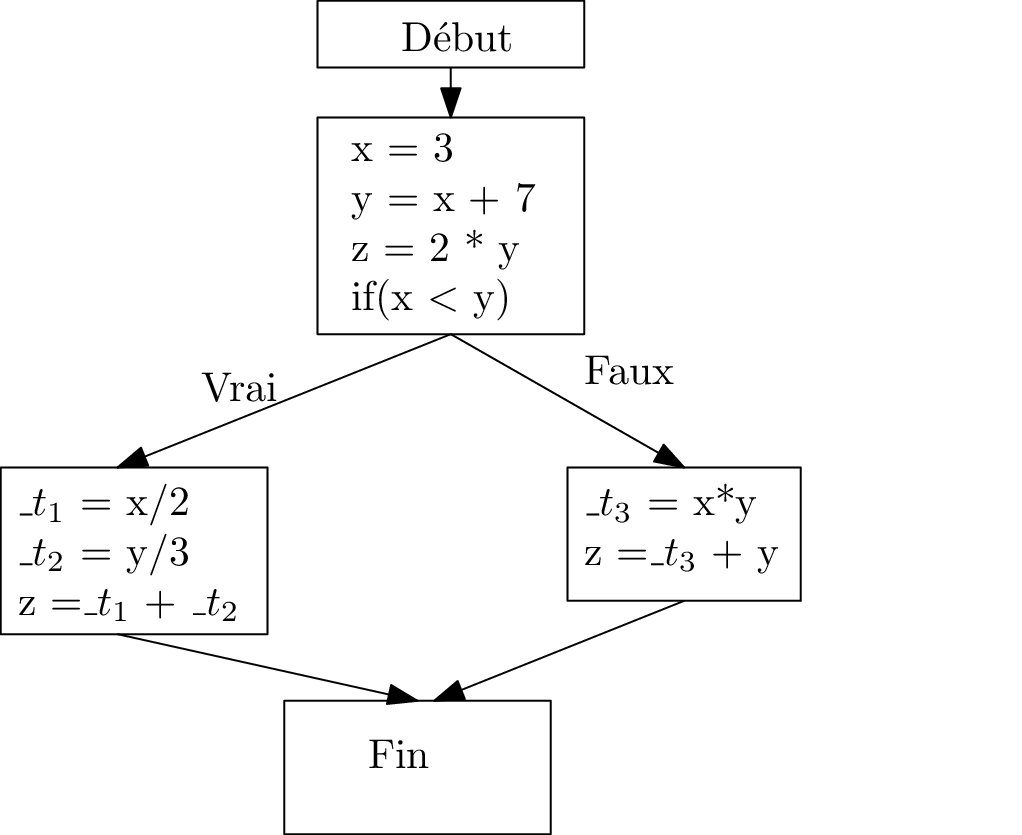
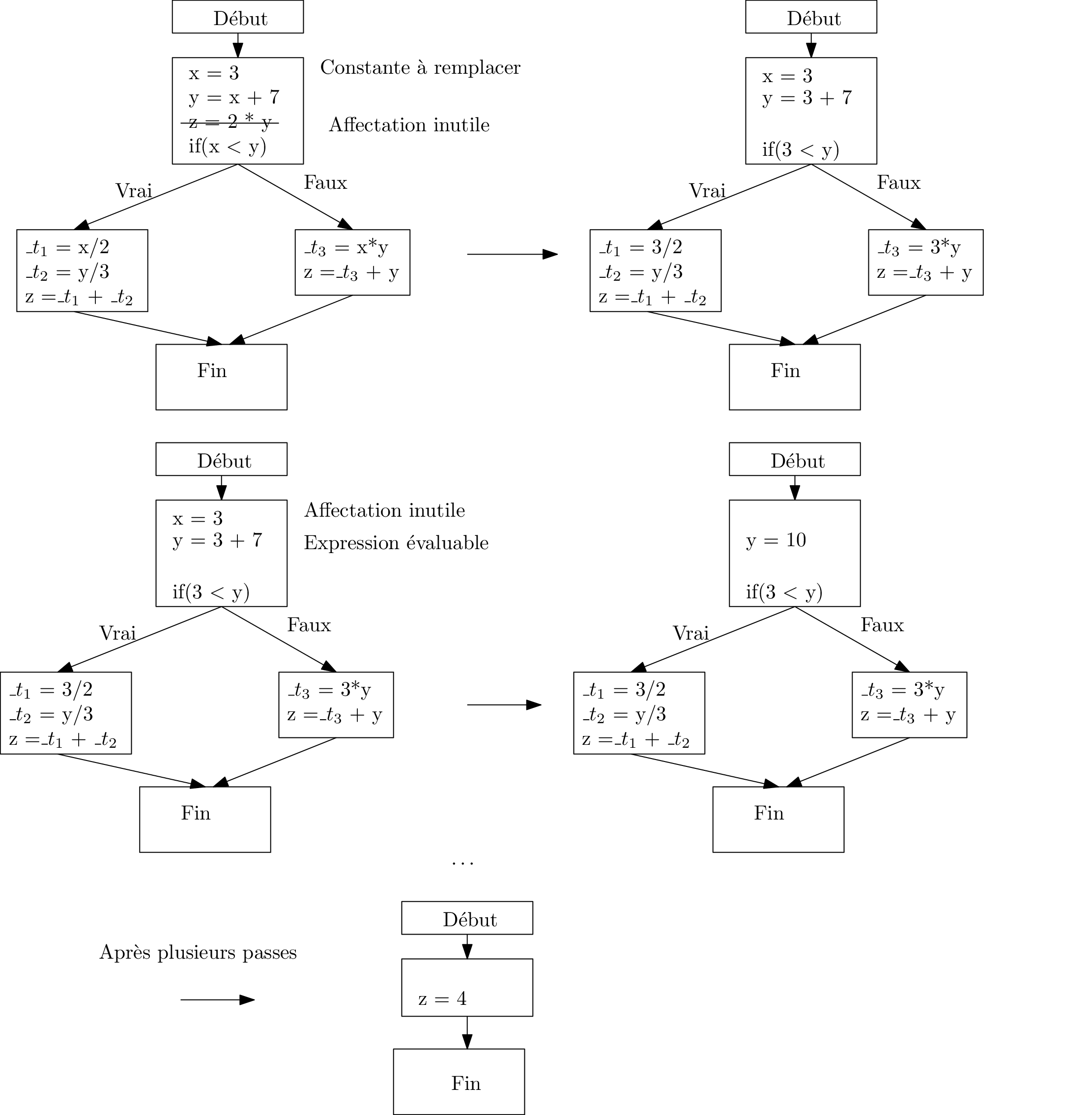
_L1:Optimisation d’un CFG
Note
Application répétée de quelques règles de simplification
- supprimer des affectations inutiles
- remplacer des constantes : int x = 3; int y = x + 2 ⇒ int x = 3 ; int y = 3 + 2;
- calculer des expressions constantes : int y = 3 + 2; ⇒ int y = 5
jusqu’à ce que plus aucune des règles ne soit applicable
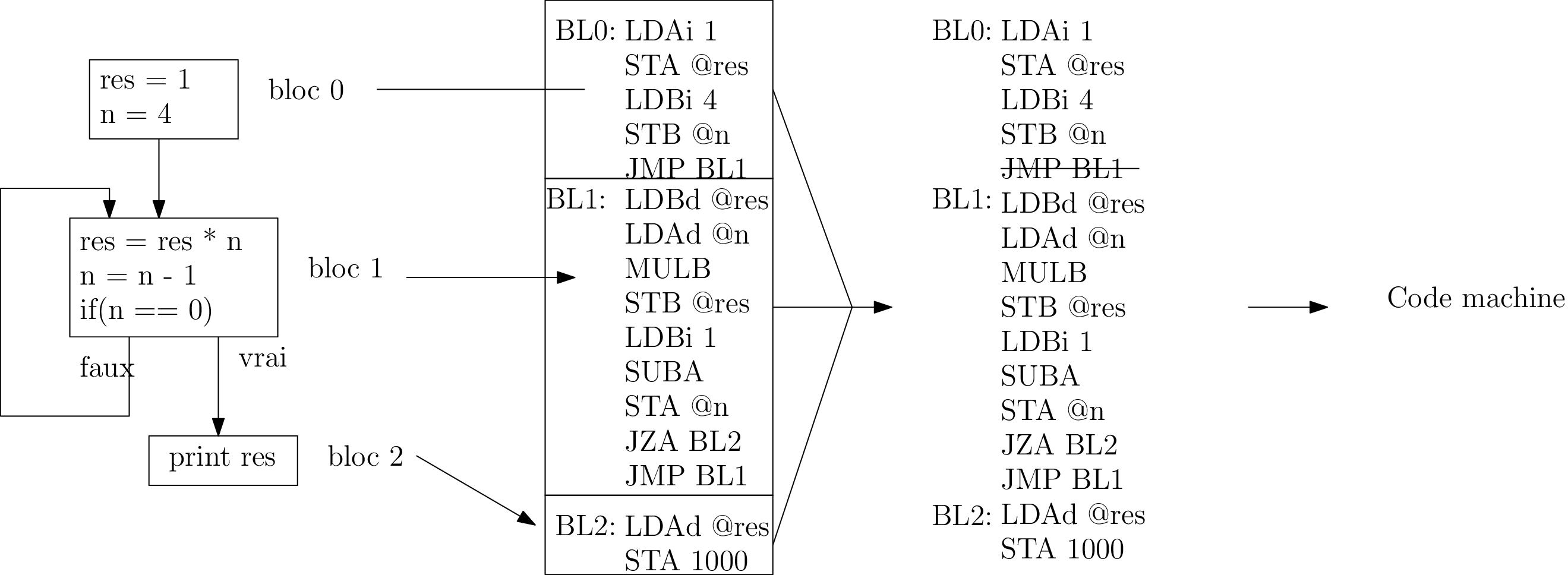
La phase de synthèse (backend)
Représentation intermédiaire ⇒ Code machine
- génération du code machine de chacun des blocs
- disposition en mémoire des blocs
- optimisations éventuelles
Et voila
Références :
- “The dragon book” Aho, Lam, Sethi, Ullman
- “Modern Compiler Implementation”, A. Appel

Produced with quarto

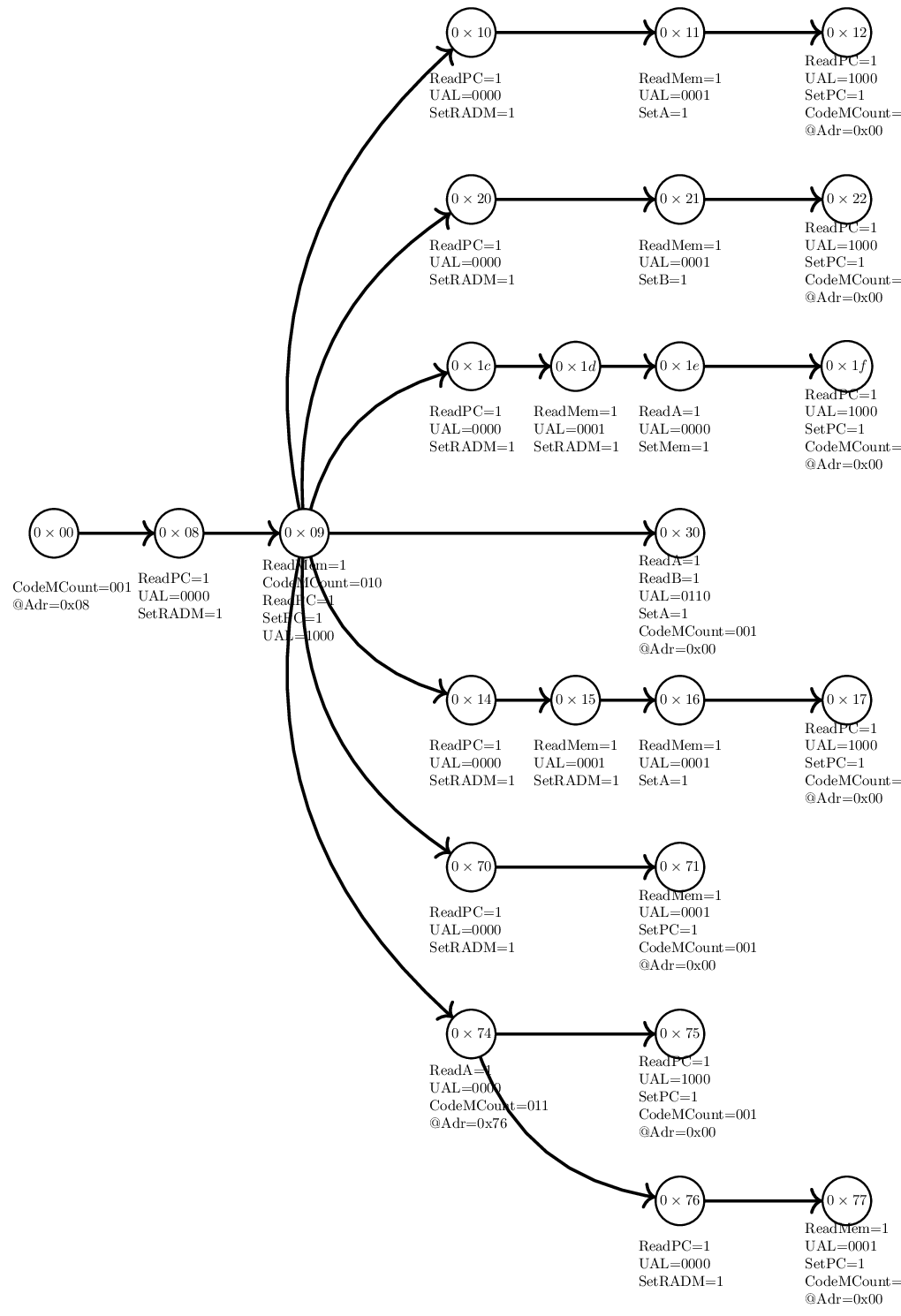






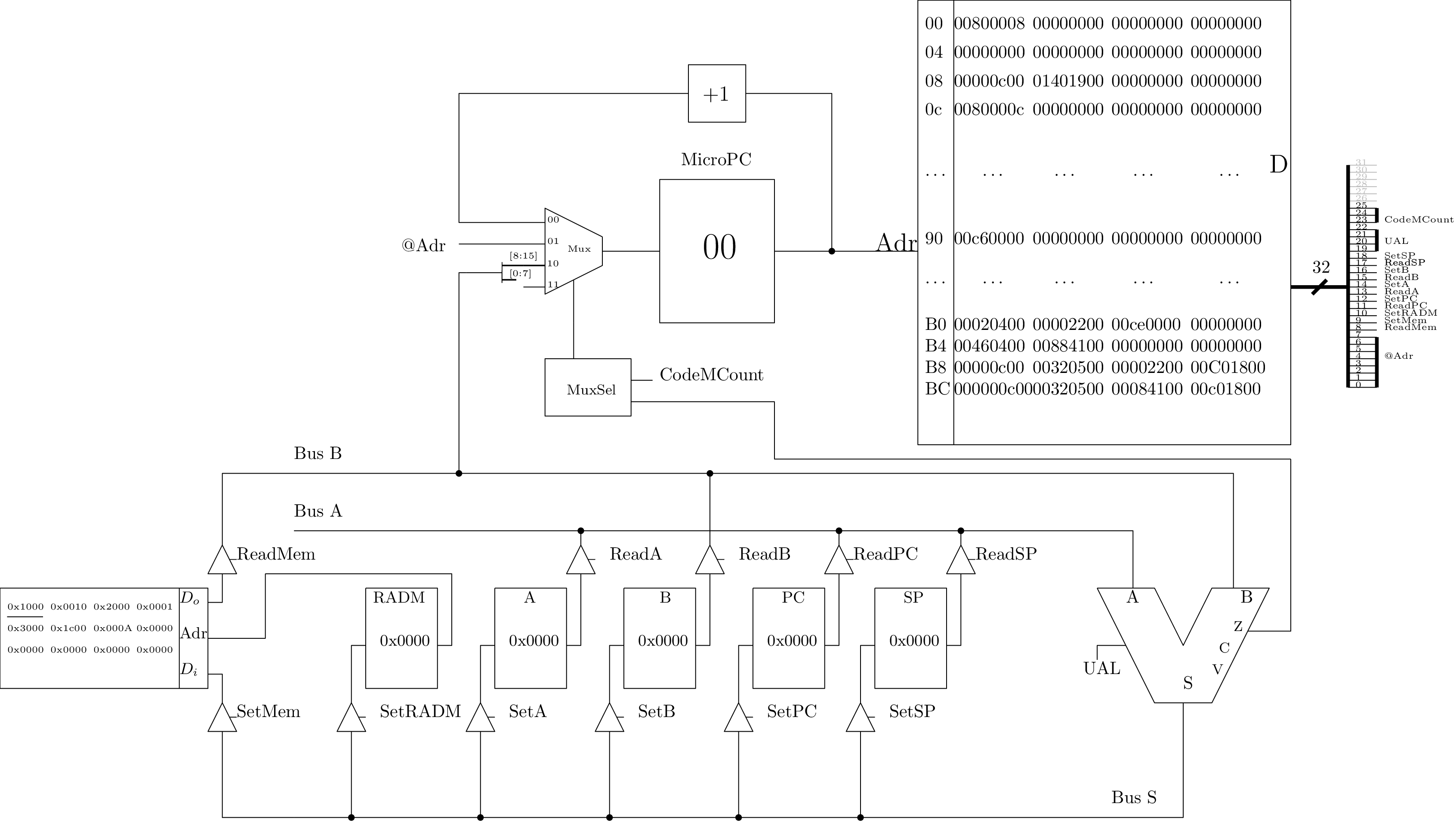
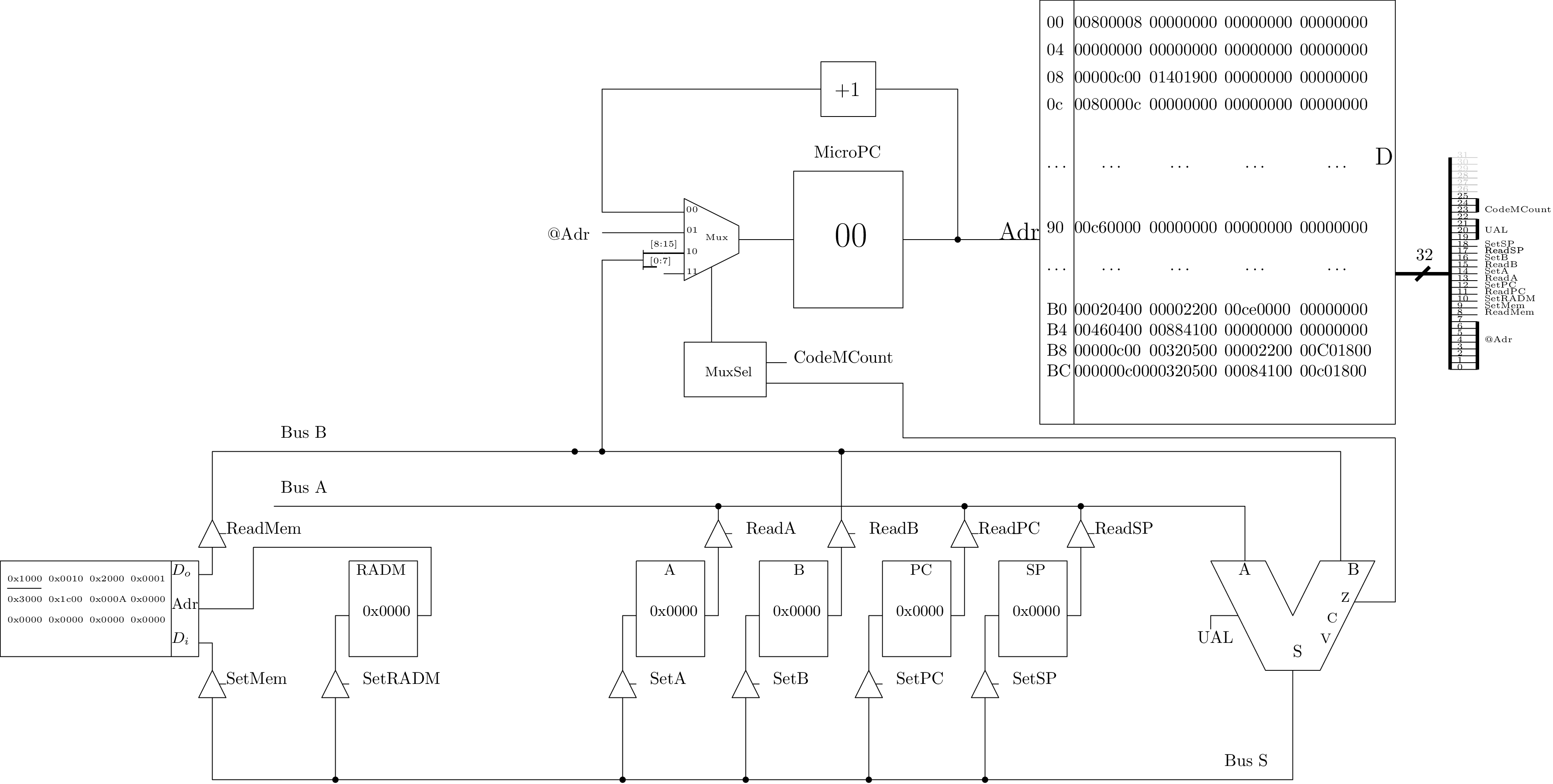






Comment faire pour simplifier la programmation ?
Ne plus écrire en code machine1
2000 0002
3000
LDBi 2
ADDA
b=2
a=a+b
et bien sûr comment faire la conversion vers le langage machine