Python pour les scientifiques

Une rapide introduction

Jeremy Fix

CentraleSupélec

Introduction

Syllabus

Module SPM-INF-002:

  • 2 CM : calcul scientifique, gestion de données et visualisation
  • 6 TPs disponibles sur https://jeremyfix.github.io/Python-for-scientists/ :
    • TP1 : manipulation de tableaux, calculs matriciels
    • TP2 : Interpolation et optimisation
    • TP3 : Traitement du signal
    • TP4 : Analyse de données avec pandas
    • TP5 : Statistiques
    • TP6 : Apprentissage automatique avec scikit-learn

Evaluation par les rendus des TPs, limite 1 semaine après le TP.

Ressources

Scientific python lectures aborde :

  • le langage python
  • Numpy, Matplotlib, Scipy,
  • des sujets avancés (interface python/C++)
  • …

Scientific python lectures

Petit tour d’horizon

L’écosystème python est très riche en librairies scientifiques :

  • Numpy pour le calcul,
  • Pandas pour l’analyse de données,
  • Scipy pour le traitement du signal,
  • Scikit-learn pour l’apprentissage automatique,
  • Matplotlib/Seaborn pour les tracés,
  • Sympy pour le calcul symbolique,

Introduction à l’interpréteur python

Les interpréteurs

Python est un langage interprété

  • Langage compilé = déjà transformé en instructions CPU
  • Langage interprété = un programme (compilé :) ) transforme “à la volée” votre code en instructions.

“à la volée”: cpython peut créer un fichier .pyc qui contient le code compilé (bytecode).

fix_jer@stollen:~$ python3
Python 3.8.10 (default, May 26 2023, 14:05:08) 
[GCC 9.4.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> l = range(100)
>>> sum(l)
4950
>>>

Les interpréteurs

Instructions CPU x86, arm.

Performances de différentes version du “même” code

Un code lent et gourmand en mémoire

l = list(range(10000000))
lsum = 0
for i in range(len(l)): 
    lsum += l[i]

Mauvais code

  • range explicité en mémoire \(\neq\) paresseuse
  • boucle for en python
  • l’accès indicé l[i] pourrait être problématique mais les listes python sont des tableaux et pas des listes chaînées

Un peu plus rapide, moins gourmand en mémoire

l = range(10000000)
lsum = 0
for li in l: 
    lsum += li

Mauvais code

  • la boucle for est exécutée en python, c’est à dire interprétée

Le “même” code mais plus efficace

Bien plus vite tout en restant paresseux en mémoire

l = range(10000000)
lsum = sum(l)

Fondamentalement différent

  • Appel de la fonction built-in sum, déjà compilée

Plus rapide mais plus gourmand avec numpy

import numpy as np

l = np.arange(10000000)
lsum = l.sum()

Un autre bénéfice de la compilation : le code vectorisé

Instructions vectorielles

  • les processeurs modernes disposent d’instructions vectorielles, e.g. AVX
  • une instruction vectorielle (SIMD : Single Instruction Multiple Data) peut appliquer la même opération sur plusieurs données (e.g. \(4\) données)
  • l’interpréteur python CPython ne supporte pas les instructions vectorisées,
  • les compilateurs, e.g. pour C++ comme gcc ou clang, réorganisent le code pour exploiter les instructions SIMD
  • les outils/librairies comme numpy, cython ou pypy compilent du code python et peuvent utiliser les instructions SIMD

Installation des packages

Environnement virtuel

Un environnement virtuel est :

  • un répertoire isolé d’installation
  • qui a vocation à ne contenir que les dépendances de votre projet en cours
  • dont la construction est documentée

Il permet la reproductibilité (Benureau and Rougier 2018), avec le contrôle des packages installés et de leurs versions.

Différentes options :

  • venv (inclus dans Python depuis la version 3.3) : python package manager, ne permet pas de changer de version de python
  • anaconda, miniconda, mamba, micromamba, etc… : system package manager. Permet de changer de version de python, installer des dépendances autres que des packages python (e.g. C++, Java, Rust, …), mais parfois un peu lourd
  • uv https://docs.astral.sh/uv : python package manager, flexible sur la version de python, ne permet d’installer que des paquets python

Exemple avec micromamba

Pour installer micromamba (en utilisateur normal):

$ "${SHELL}" <(curl -L micro.mamba.pm/install.sh)

Pour construire un environnement virtual local dédié :

$ micromamba create -p ./mon_env python=3.13
$ micromamba activate ./mon_env

Pour installer des dépendances :

$ micromamba install numpy pandas matplotlib
$ micromamba install numpy=2.0.1

On peut exporter, recharger, etc.. un environnement.

Exemple avec uv

Pour installer uv (en utilisateur normal) :

$ curl -LsSf https://astral.sh/uv/install.sh | sh

Pour construire un environnement virtuel local dédié :

$ uv venv --python 3.13 mon_venv
$ source mon_venv/bin/activate

Pour installer des dépendances :

$ uv pip install numpy pandas matplotlib
$ uv pip install numpy==2.0.1
$ uv pip install -r requirements.txt
$ uv pip install . # pour un projet avec un pyproject.toml par exemple

Environnement de développement

VS Code

Warning

Vous devez utiliser un Integrated Development Environment (IDE)

Suggestion : utilisez Visual Studio Code + tout son environnement de plugins qui permet :

  • de gérer votre projet (création, organisation des fichiers)
  • disposer de la coloration syntaxique, complétion de code, etc…
  • mettre en place un environnement virtuel et exécuter le code dans cet environnement
  • utiliser des notebooks jupyter
  • interagir avec git

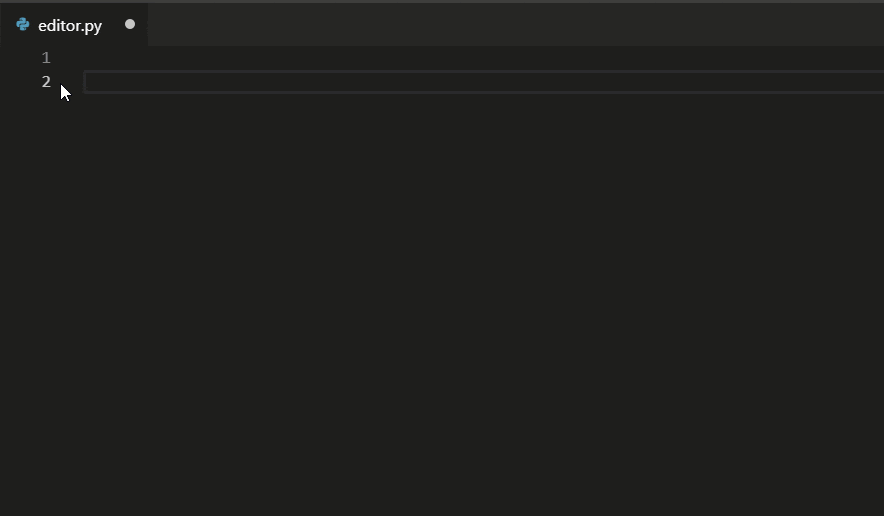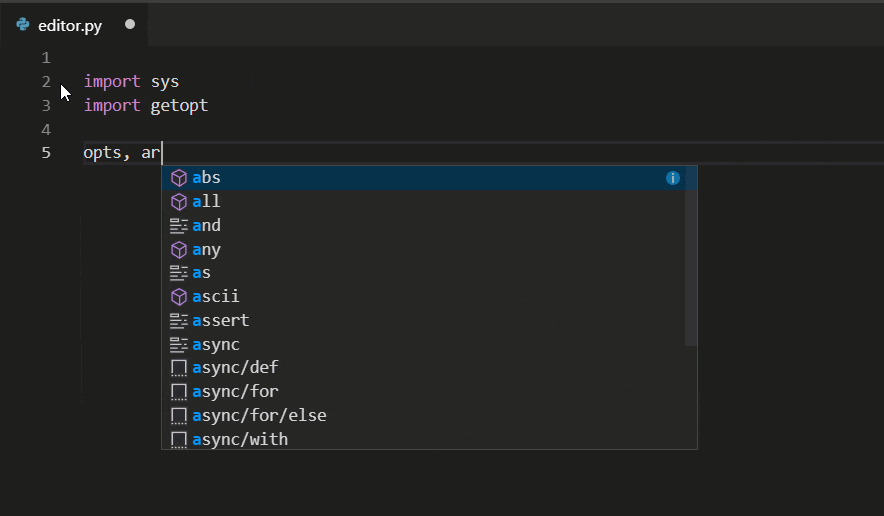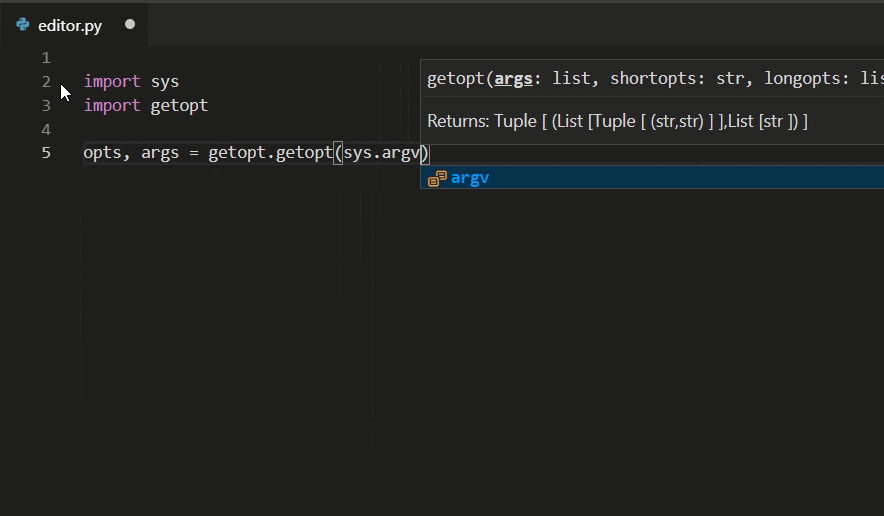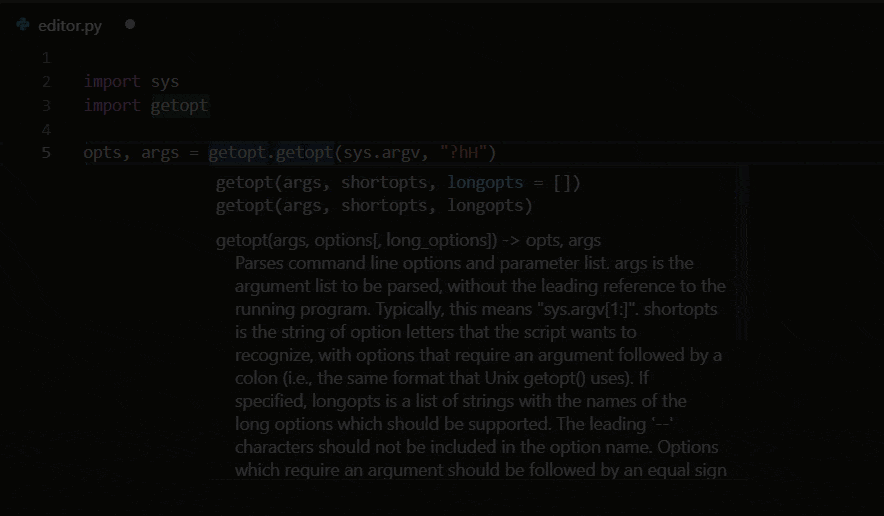
VS Code https://code.visualstudio.com/docs/languages/python

=> Démo avec Venv

Jupyter notebook/lab

On peut également travailler avec des notebooks jupyter.

$ uv pip install jupyter
$ jupyter notebook

Fonctionnalités :

  • supporte des noyaux python, c++, R, …
  • permet de combiner du texte et du rendu
  • permet d’inclure des widgets dynamiques (e.g. sliders)

Voir ces exemples à essayer dans le navigateur, e.g. le simulateur de l’attracteur de Lorentz

Notebook jupyter, démo Lorenz.ipynb

Notebook jupyter, démo Lorenz.ipynb

Python : bases

Rappels de syntaxe de base

  • ATTENTION à l’indentation
  • types int, float, bool, set
  • types “séquence” immutables: str, tuple
  • type “séquence” mutable : list
  • type séquence clé/valeur : dict
  • interroger le type type(x), tester le type isinstance(x, letype), connaître les méthodes applicables dir(x)
  • opérateur d’affectation x = 3, walrus
with open(fname, 'r') as fh:
    while((line:=fh.readline()) != ''):
        print(line.rstrip())
  • opérateurs arithmétiques (+, -, /, *), et logiques (and, or, not)
  • branchements conditionnés if ... else .. if ... elif ... else
  • opérateur ternaire, lambda fonction
syr = lambda x: x//2 if x%2 == 0 else 2*x+1

x = 18 
syr(x)
  • boucles for x in [1, 2, 3]:, while condition:

Rappels de syntaxe de base

Sur les listes

l = [1, 2, 3]

# Listes par compréhension
l2 = [li**2 for li in l]
lpair = [li for li in l if li % 2 == 0]

# Slicing, indexation
l[start:step:stop]

# E.g. : inversion
l[::-1]

Faire attention aux constructions du type :

l = .... # une séquence
lsum = 0
for i in range(len(l)):
  lsum += l[i]

Complexité en temps en \(O(|L|^2)\) pour une liste chaînée. Complexité en temps en \(O(|L|)\) pour un tableau.

Rappels de syntaxe de base

Les générateurs

Une construction de liste par compréhension est exécutée à la déclaration.

Pour économiser de la mémoire (e.g. permettant de représenter d’énormes structures), on peut utiliser des générateurs

l = [i**2 for i in range(10000000)] # Liste créée tout de suite

lsum = sum(l)

# Avec des générateurs
l = (i**2 for i in range(10000000)) # Liste créée tout de suite
sum(l)

Rappels de syntaxe de base

Sur les fonctions

Définition d’une fonction : def fname():


# Une fonction à 3 arguments
def f(a, b, c):
  ....
  return ...


f(1, 2, 3)

On peut utiliser un nombre variable d’arguments positionnels *args et/ou nommés **kwargs (kwargs = keyword arguments). Voir Python args and kwargs.


def f(*args, **kwargs):
  ....

# args = [1, 2, "a"]
# kwargs = {"bidule": "machine", "chose": 3}
f(1, 2, "a", bidule="machine", chose=3)

Les lambda fonctions allègent la déclaration des fonctions :

fsq = lambda x: x**2

fsq(2)

Modificateurs de fonctions : les décorateurs

Voir https://www.pythoncheatsheet.org/cheatsheet/decorators

@your_decorator
def say_hi(name):
  print("Hi ! My Name is "+ name)

def your_decorator(func):
  def wrapper(*args,**kwargs):
    # Do stuff before func...
    result = func(*args,**kwargs)
    # Do stuff after func..
    return result
  return wrapper
@CountCallNumber
def say_hi(name"):
  print("Hi ! My Name is "+ name)

class CountCallNumber:
  def __init__(self, func):
    self.func = func
    self.call_number = 0

  def __call__(self, *args, **kwargs):
    self.call_number += 1
    print("This is execution number " + str(self.call_number))
    return self.func(*args, **kwargs)

Rappels de syntaxe de base

Loguer avec print: Pour déboguer un programme, on utilise bien souvent des print(...)

Que l’on peut combiner avec des f-strings :

def sqsum(l: list):
  return sum((li**2 for li in l))

l = [1, 2, 3]
print(f"La somme des carrés de {l} est : {sqsum(l)}")

Que l’on peut combiner avec des options de formattage :

import math

p = math.pi
# Produit un label de longueur 10, avec pi arrondi au millième
pilabel = f"La valeur de pi arrondi au millième est {math.pi:10.3f}"

print(pilabel)

Loguer avec logging : On peut aussi utiliser des loggers du module logging :

import logging

logging.basicConfig(format="%(levelname)s - %(asctime)s: %(message)s", 
                    datefmt= "%d/%m/%y %H:%M:%S", level=logging.INFO)

logging.info("Une info")
logging.warning("Un warning")
logging.error("Une erreur")

logging.basicConfig(filename="monlog.log",
                    format="%(levelname)s - %(asctime)s: %(message)s", 
                    datefmt= "%d/%m/%y %H:%M:%S", level=logging.INFO)

Lire/ecrire dans un fichier

De manière générale sur un texte en ASCII :

Lecture, avec un with statement:

with open("monfichier", "r") as fh:
  while True:
    line= fh.readline()
    if line == '':
      break

    process(line)

# Ou avec walrus
with open(fname, 'r') as fh:
    while((line:=fh.readline()) != ''):
      process(line)

Ecriture :

with open("monfichier", "w") as fh:
  montexte = f"La valeur de pi arrondi au millième est {math.pi:10.3f}"
  fh.write(montexte)

ATTENTION C’est une très mauvaise idée de stocker en ASCII des données numériques.

La valeur “1.23439949959” en ASCII occupe \(13 \times 8 = 104 bits\). Alors qu’un flottant peut occuper \(64\), \(32\), \(16\) bits.

Si ce sont des tableaux de valeurs, utilisez numpy.savez.

Vous pouvez aussi construire votre propre format de fichier et utiliser fh.seek(), fh.read(num_bytes), struct.pack(), struct.unpack(). Voir [struct](https://docs.python.org/3/library/struct.html]

Sur des formats spécifiques yaml, xml, json, utilisez des parsers écrit pour le yaml, xml, json

Python: classes, threads, UI, packing

Un problème pour se motiver

Problème Simuler un système d’Ising (Sethna (2006), Hayes (2000)). Moment magnétique des atomes arrangés sur une grille régulière \(\sigma_i \{-1, 1\}\). Pour une grille finie, il existe un nombre fini de configurations mais avec des dynamiques intriguantes.

La probabilité d’occuper un état du système \(\sigma\) est \(P(\sigma) = \frac{1}{Z}\exp(-\beta E(\sigma))\), avec

\[ E(\sigma) = -\sum_{i < j} J_{i,j} \sigma_i \sigma_j \]

  • transition déterministe si l’énergie globale diminue, \(\Delta E < 0\),
  • transition stochastique si l’énergie augmente \(\Delta E > 0\), avec probabilité \(\exp(-\beta \Delta E) \in [0, 1]\)

Système de Ising

Système de Ising

Il existe des transitions de phase, en particulier pour \(\beta \approx 2.269\).

Voir la description complète du système sur https://tutos.metz.centralesupelec.fr/TPs/Intro-Python/index.html#an-example-project-simulating-the-ising-model

Les classes

Concept fondamental de programmation orientée objet (OOP).

  • Un objet = des attributs modifiables par des méthodes qui forment un tout cohérent. On parle aussi de classe,
  • Une réalisation d’un objet est appelée une instance,
  • peut être organisé de manière hiérarchique,
  • peut redéfinir/spécifier des opérations

On peut construire une instance d’un objet :

class MaClasse:
  
  # Constructeur
  def __init__(self, ...):
    pass

On dispose également de beaucoup de méthodes spéciales : __lt__, __add__, __str__, …

On peut construire une hiérarchie de classes, on doit alors appeler le constructeur de la classe mère.

Illustrations de la programmation orientée objet

Problème Écrire un évaluateur d’expressions mathématiques.

from abc import ABC, abstractmethod

class Expression(ABC):
    @abstractmethod
    def __str__(self):
        pass

    @abstractmethod
    def __call__(self, env):
        pass

class Variable(Expression):
    def __init__(self, name):
        self.name = name

    def __call__(self, env):
        return env[self.name]

    def __str__(self):
        return self.name
class BinaryOp(Expression):
    def __init__(self, fun, left, right):
        self.fun = fun
        self.left, self.right = left, right

    def __call__(self, env):
        return self.fun(self.left(env), self.right(env))

class Add(BinaryOp):
    def __init__(self, left, right):
        super().__init__(lambda x, y: x+y, left, right)

    def __str__(self):
        return f"({self.left} + {self.right})"

class Multiply(BinaryOp):
    def __init__(self, left, right):
        super().__init__(lambda x, y: x*y, left, right)

    def __str__(self):
        return f"({self.left} * {self.right})"

Exemple

# Exemple usage
# expr = parse("3 * x + 2")

expr = Add(Multiply(Constant(3), Variable('x')), Constant(2))

print(expr)  # (3 * x + 2)
print(expr.evaluate({'x': 5}))  # 17

Les classes

On décompose le projet en \(3\) classes :

  • un simulateur qui s’occupe de la physique
  • une interface en ligne de commande Console
  • une interface graphique IsingGUI

Diagramme de classes

Diagramme de classes

Les threads ?

Un programme peut déclencher plusieurs fils d’exécutions, les threads. Ici :

  • un thread pour le simulateur
  • un thread pour l’interaction avec l’utilisateur (le principal)

Cela permet à la simulation de continuer à tourner même si l’utilisateur n’interagit pas.

class Console(object):
    def __init__(self, simu):
        self.simulator = simu

    def ask_for_interaction(self):
      ...

    def on_choice(self, choice):
      ...

    def start(self):
        """
        The main loop
        """
        while self.keep_alive:
            choice = self.ask_for_interaction()
            self.on_choice(choice)
import threading
class Simulator(threading.Thread):

    def __init__(self, lattice_size, kT):
        threading.Thread.__init__(self)
        self.lock = threading.RLock()
        self.spins = np.random.random((lattice_size, lattice_size)) > 0.5

    def run(self):
        while self.is_kept_alive():
            if self.running:
                self.step()

    def stop(self):
        with self.lock:
            self.keeps_alive = False

    def get_spins(self):
        with self.lock:
            return self.spins.copy()

Au lieu des threads, on aurait pu utiliser du multiprocessing.

Installation et exécution

Installation (grâce au setup.py)

uv venv /tmp/venv
source /tmp/venv/bin/activate
uv pip install -e ising_package

Exécution

python -m ising.console
python -m ising.qtgui

Packaging du projet

Le projet est packagé avec setuptools.

La python packaging authority (pypa) maintient un tutorial sur le packaging, voir https://setuptools.pypa.io/en/latest/userguide/quickstart.html

Le packaging peut se faire avec un setup.py :

import setuptools

with open("README.md", "r") as fh:
    long_description = fh.read()

setuptools.setup(
    name="Ising",
    version="1.0",
    author="CentraleSupelec",
    author_email="Jeremy.Fixcentralesupelec.fr",
    description='A simulator of the Ising model with '
                'the Metropolis algorithm',
    long_description=long_description,
    long_description_content_type="text/markdown",
    url='http://tutos.metz.centralesupelec.fr/Intro_Python',
    packages=setuptools.find_packages(),
    classifiers=[
        "Programming Language :: Python :: 3",
        "License :: OSI Approved :: MIT License",
        "Operating System :: OS Independent",
    ],
    python_requires='>=3.6',
    install_requires=['numpy', 'scipy', 'PyQt5', 'matplotlib', 'opencv-python-headless']
)

Mais pourrait aussi utiliser pyproject.toml.

Et vous pourriez déposer votre librairie sur pypi, ou conda.

Calcul scientifique avec Numpy

Introduction

Numpy : Numerical Python

  • Librairie C++ avec un wrapper python,
  • qui offre des tableaux multi-dimensionnels et des opérations optimisées
NumPy is the fundamental package for scientific computing in Python. It is a Python library that provides a multidimensional array object, various derived objects (such as masked arrays and matrices), and an assortment of routines for fast operations on arrays, including mathematical, logical, shape manipulation, sorting, selecting, I/O, discrete Fourier transforms, basic linear algebra, basic statistical operations, random simulation and much more.
import numpy as np

Création de tableaux

Plusieurs approches pour créer un tableau Numpy :

  • à partir d’une liste (éventuellement de listes de listes de ..)
  • à partir de fonctions dédiées : np.zeros, np.ones, np.arange, np.linspace, np.random.rand, etc.
  • à partir de fichiers : np.loadtxt, np.genfromtxt, np.load, etc.
# Tableau 1D de taille (5, )
np.array([1, 2, 3, 4, 5])

# Tableau 2D de taille (2, 3)
np.array([[1, 2, 3], [4, 5, 6]])

# Tableau 2D de taille (3, 4) rempli de zéros
np.zeros((3, 4))

# Tableau 6D de taille (2, 3, 4, 5, 6, 7) rempli de uns
np.ones((2, 3, 4, 5, 6, 7))

# Tableau 1D de 0 à 10 par pas de 2
np.arange(0, 10, 2)

# Tableau 1D de taille (5, ) avec des valeurs entre 0 et 1
np.linspace(0, 1, 5)

# Tableau 2D de taille (3,3) avec des valeurs aléatoires entre 0 et 1
np.random.rand(3, 3)

Propriétés des tableaux

Les tableaux ont :

  • une forme (shape) : nombre de dimensions et taille dans chaque dimension,
  • un type (dtype) : type des éléments du tableau,
  • un nombre d’éléments (size) : nombre total d’éléments dans le tableau,
  • un nombre de dimensions (ndim) : nombre de dimensions du tableau.
a = np.array([[1, 2, 3], [4, 5, 6]])
print(a)

print("Shape:", a.shape)      # (2, 3)
print("Dtype:", a.dtype)      # int64 (ou int32 selon la plateforme)
print("Size:", a.size)        # 6
print("Ndim:", a.ndim)        # 2

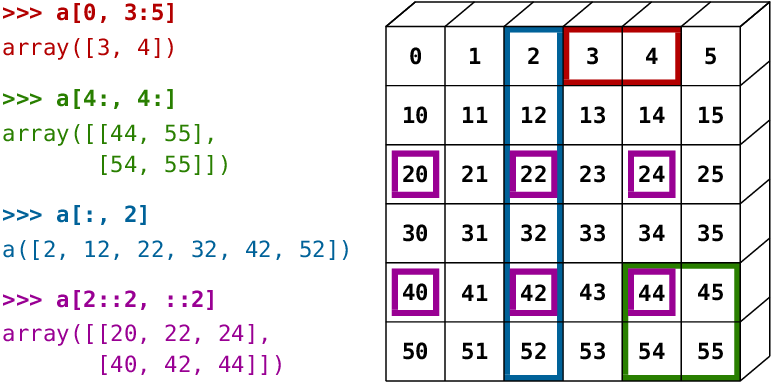
Accès aux éléments

On accède aux éléments :

  • par index,
  • par slicing, en utilisant la syntaxe python start:stop:step,
  • par masquage booléen

Illustration de slicing de https://lectures.scientific-python.org/intro/numpy/array_object.html

Illustration de slicing de https://lectures.scientific-python.org/intro/numpy/array_object.html

Pour l’efficacité en mémoire et temps:

  • le slicing crée une vue sur le tableau original, pas une copie.
  • Mais, le fancy indexing crée une copie, pas une vue.

On peut le vérifier avec l’attribut base

a = np.array([[1, 2, 3], [4, 5, 6]])

# Accès par index
# Premier élément de la première ligne
a[0, 0]  # 1

# Accès par slicing
# Deuxième ligne
# Equivalent à a[1]
a[1, :]  # [4 5 6]

# Première colonne
a[:, 0]  # [1 4]

# Toutes les lignes, colonnes d'indice pair
a[:, ::2] #
a[:, ::2] = 0 # Modifie a

# Masquage booléen : fancy indexing
mask = a > 3 # np.array de dtype bool
b = a[mask]  # [4 5 6]
b[0] = 10    # Ne Modifie pas a

Accès aux éléments (suite)

Ne jamais faire

a = np.array([[1, 2, 3], [4, 5, 6]])

for i in range(a.shape[0]):
  for j in range(a.shape[1]):
    a[i, j] = 0

mais utiliser l’ellipsis :

a = np.array([[1, 2, 3], [4, 5, 6]])

a[...] = 0

Manipulations sur la forme des tableaux

On peut modifier la forme d’un tableau par :

  • np.reshape : retourne une vue du tableau avec une nouvelle forme,
  • np.flatten ou np.ravel : retourne une copie ou une vue du tableau aplati (1D),
  • np.transpose : retourne une vue du tableau transposé,
  • np.pad : ajoute une bordure autour du tableau.
  • np.expand_dims, x = x[np.newaxis, :] : ajoute une nouvelle dimension.

On peut combiner/diviser plusieurs tableaux par :

  • np.concatenate : concatène plusieurs tableaux le long d’un axe,
  • np.stack : empile plusieurs tableaux le long d’un nouvel axe,
  • np.hstack et np.vstack : concatène horizontalement ou verticalement plusieurs tableaux.
  • np.split, np.hsplit, np.vsplit : divise un tableau en plusieurs sous-tableaux.

On peut permuter les éléments d’un tableau par :

  • np.transpose, np.swapaxes
  • np.roll

Opérations arithmétiques sur les tableaux

Les opérations arithmétiques sont appliquées élément par élément +, ‘/’, -, *. Il existe également les opérations logiques.

a = np.array([[1, 2, 3], [4, 5, 6]])
b = np.array([[10, 20, 30], [40, 50, 60]])

# Addition  
c = a + b  # [[11 22 33] [44 55 66]]

# Soustraction
d = b - a  # [[9 18 27] [36 45 54]]

# Multiplication terme à terme
e = a * b  # [[10 40 90] [160 250 360]]

# Division terme à terme
f = b / a  # [[10. 10. 10.] [10. 10. 10.]]

Attention : * est le produit terme à terme, pas le produit matriciel. Le produit matriciel est obtenu par np.matmul ou simplement @

Illustration - Système de GrayScott

Problème Simuler le système de réaction-diffusion de GrayScott dont l’évolution des champs spatialisés \(u(x,t)\), \(v(x,t)\), \(x\in \mathbb{R}^2\) est régie par :

\[ \begin{eqnarray*} \frac{\partial u}{dt}(x,t) &=& D_u \nabla^2 u(x,t) - u(x,t) v^2(x,t) \\ & &+ F(1-u(x,t))\\ \frac{\partial v}{dt}(x,t) &=& D_u \nabla^2 v(x,t) + u(x,t) v^2(x,t) \\ && - (F+k) v(x,t) \end{eqnarray*} \]

def step(ut_1, vt_1, Du, Dv, F, k):
  uvv = ut_1 * vt_1**2
  lu = laplacian(ut_1)
  lv = laplacian(vt_1)
  ut[...] = ut_1 + dt * (Du * lu - uvv + F*(1-ut_1))
  vt[...] = vt_1 + dt * (Dv * lv + uvv - (F + k) * vt_1)

def laplacian(src):
  """
  u is a 2D nd array
  """
  padded_src = np.pad(src, pad_width=1, mode="constant")  # zero padding src
  laplacian = (
      0
      + padded_src[0:-2, 1:-1]
      + 0
      + padded_src[1:-1, 0:-2]
      - 4 * padded_src[1:-1, 1:-1]
      + padded_src[1:-1, 2:]
      + 0
      + padded_src[2:, 1:-1]
      + 0
  )

  return laplacian[1:-1, 1:-1]

avec \(\nabla^2\) le laplacien discret :

\[ \nabla^2 u(x,y) = \frac{u(x-\delta, y) + u(x+\delta, y) + u(x, y-\delta) + u(x, y+\delta) - 4 u(x,y)}{\delta^2} \]

Illustration - Système de Grayscott

$ uv venv /tmp/venv
$ source /tmp/venv/bin/activate
$ uv pip install numpy scipy opencv-python
$ python cv2_grayscott 4

Grayscott simulation

Grayscott simulation

Fonctions Mathématiques

Les fonctions Mathématiques s’appliquent sur tout les éléments, e.g. np.exp, np.sin, np.log, etc mais également les puissances.

e.g. Calcul d’une gaussienne centrée en \(x=2\) avec écart-type \(\sigma=0.5\)

x = np.linspace(0, 4, 100)
sigma = 0.5
gauss = (1/(sigma * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x - 2) / sigma) ** 2)

On peut également calculer (selon un axis=..):

  • la somme : np.sum,
  • le plus petit/grand : np.min, np.max, np.argmin, np.argmax,
  • la moyenne : np.mean \(\frac{1}{N} \sum_i X[..., i, ...]\), l’écart type np.std \(\sqrt{\frac{1}{N} \sum_i (X[..., i, ...] - \mu_i)^2}\)
  • la covariance : np.cov \(\sum_i (x_i - \mu)^T (x_i - \mu)\)
  • …

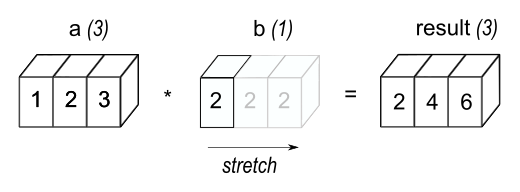
Broadcasting

Le broadcasting est un mécanisme qui permet d’effectuer des opérations entre des tableaux de formes différentes.

Numpy “étend” automatiquement les dimensions des tableaux pour qu’ils soient compatibles pour l’opération.

De la documentation sur le broadcasting

La règle : des opérations sur deux tableaux sont applicables si les dimensions sont compatibles.

Les dimensions sont compatibles si, 1) les tableaux ont le même nombre de dimensions, 2) partant de la droite (des dimensions)

  • les dimensions sont égales
  • ou sont différentes mais l’une d’elle est égale à \(1\) \(\rightarrow\) Broadcast

Sinon vous obtiendrez l’exception ValueError: operands could not be broadcast together

Broadcasting - example

Par exemple, on souhaite calculer la valeur d’une fonction gaussienne \(f(x)\) centrée en \(\mu\in\mathbb{R}^2\), sur une grille régulière centrée sur \(\mu\) :

\[ \forall x \in \mathbb{R}^2, f(x) = \frac{1}{\sigma \sqrt{2\pi}} \exp(\frac{- \|x - \mu\|_2^2}{2\sigma^2}) \]

if __name__ == '__main__':
    mu = np.array([1, 2])
    sigma = 0.3
    step = 0.1
    Nsteps = 10
    X = gaussian(mu, sigma, step, Nsteps)

def gaussian(mu: np.ndarray, sigma: float, step: float, Nsteps: int) -> np.ndarray:
    # Generate the regular grid
    # (-N, -(N-1), ..., -1, 0, 1, ..., N-1, N) * step
    intsteps = (np.arange(Nsteps) + 1)
    deltasteps = np.concatenate([-intsteps[::-1], [0], intsteps]) * step

    # Generate the steps centered on mu
    # mu is (2, ), we use broadcasting on mu and deltasteps to generate
    # mu (2, 1) + deltasteps(1, M) => mu + deltasteps is (2, M)
    mu_delta = mu[:, np.newaxis] + deltasteps[np.newaxis, :]

    # Generate the meshgrid with this values
    # X and Y are of shape (2*Nsteps + 1, 2*Nsteps + 1)
    X, Y = np.meshgrid(mu_delta[0], mu_delta[1])

    # Concatenate the X, Y matrices
    # xy is  (( (2*Nsteps + 1) * (2*NSteps + 1), 2)
    xy = np.concatenate((X.ravel()[:,np.newaxis], Y.ravel()[:, np.newaxis]), axis=1)

    # Compute tha gausian values
    # To compute the distance between the grid points is computed between xy and mu
    # To broadcast, we do :   xy (M, 2) - mu(1, 2)
    dist = ((xy - mu[np.newaxis, :])**2).sum(axis=1)
    values = 1.0 / (2.0 * sigma * np.sqrt(2.0 * np.pi)) * np.exp(- dist / (2.0 * sigma**2))
    
    # Values is of shape (( (2*Nsteps + 1) * (2*NSteps + 1), ) that we reshape as 
    # (2*Nsteps + 1, 2*Nsteps + 1)
    values = values.reshape((2*Nsteps + 1, 2*Nsteps + 1))

    return values

Algèbre linéaire

Numpy supporte bien évidemment toutes les routines utiles en algèbre linéaire, dans le sous-package np.linalg:

  • produit matriciel , matrice-vector : np.dot
  • calcul de la trace np.linalg.trace,
  • calcul de l’inverse : np.linalg.inv, du déterminant np.linalg.det
  • calcul des normes : np.norm - norme \(p\) pour un vecteur \((\sum_i x_i^p)^{1/p}\), Frobenius pour une matrice,
  • diagonalisation, valeurs propres, vecteurs propres : np.linalg.eig
  • décompositions de Cholesky np.linalg.cholesky \(X = L L^T\) (L triangulaire inférieure), SVD np.linalg.svd \(X = U S V^T\)

Algèbre linéaire - illustrations

Moindres carrés régularisés Soit \(n, m \in \mathbb{N}\), \(A\in \mathbb{R}^{n,m}\), \(b\in \mathbb{R}^{n}\), trouver \(x \in \mathbb{R}^m\) qui minimise :

\[ argmin_x J(x) = \|A x - b\|_2^2 = \sum_{i=0}^{n-1} (\sum_{j=0}^{m-1} a_{i,j}x_j - b_i)^2 \]

En fonction du range de \(A\), il peut exister une infinité de solution. Si \(A\) est singulière, une solution est obtenue en résolvant le problème des moindres carrés régularisés \(argmin_x J(x) + \lambda \|x\|_2^2\) , \(\lambda \in \mathbb{R}^+\) :

\[ x = (A^T A + \lambda \mathbf{I})^{-1} A^T b \]

Avec numpy :

import numpy as np

def rls(A: np.ndarray, b: np.ndarray, lbd: float) -> np.ndarray:
    n, m = A.shape
    inv = np.linalg.inv(A.T@A + lbd * np.eye(m))
    x = np.dot(inv@A.T, b)
    return x

if __name__ == '__main__':
    n, m = 3, 4
    A, b = np.random.random((n, m)), np.random.random((n,))
    lbd = 0.001

    x = rls(A, b, lbd)
    print(x)

Algèbre linéaire - PCA

Analyse en composantes principales Soit \(N\) vecteurs \(x_i \in \mathbb{R}^d\), trouver le vecteur \(w_0 \in \mathbb{R}^d\) et \(r\) vecteurs de projections \(w_j\) qui minimisent l’erreur de reconstruction :

\[ \begin{align} \min_{\{w_0, w_1, ..w_r\} \in \mathbb{R}^d} \sum_{i=0}^{N-1} \left|x_i - (w_0 + \sum_{j=1}^r (w_j^T (x_i-w_0))w_j )\right|_2^2 \end{align} \]

sujet à la contrainte \(\forall i, j \geq 1, w_i^T w_j = \delta_{i,j}\).

PCA

PCA

Algèbre linéaire - PCA

Algorithme:

  1. Centrer vos données \(\widetilde{x}_i = x_i - \bar{x}\)
  2. Construire la matrice \(\widetilde{\mathbf{X}} = \begin{bmatrix} \widetilde{x}_0^T \\ \dots \\ \widetilde{x}_{N-1}^T\end{bmatrix}\)
  3. Calculer les \(r\) vecteurs propres normalisés associés aux plus grandes valeurs propres de \(\widetilde{\mathbf{X}}^T\widetilde{\mathbf{X}}\)

Implémentation naïve https://github.com/rougier/ML-Recipes

class PCA:
  def fit(self, X):
    '''
    Performs the PCA of X and stores the principal components.
    The datapoints are supposed to be stored in the row vectors of X.
    It keeps only the n_components projection vectors, associated
    with the n_components largest eigenvalues of the covariance matrix X.T X
    '''

    # Center the datapoints
    self.centroid = np.mean(X, axis=0)

    # Computes the covariance matrix
    sigma = np.dot((X - self.centroid).T, X - self.centroid)

    # Compute the eigenvalue/eigenvector decomposition of sigma
    eigvals, eigvecs = np.linalg.eigh(sigma)

    # Note :The eigenvalues returned by eigh are ordered in ascending order.

    # Stores the n_components eigenvectors/eigenvalues associated
    # with the largest eigen values
    #self.eigvals = eigvals[-self.n_components:]
    #self.eigvecs = eigvecs[:, -self.n_components:]

    # Stores all the eigenvectors/eigenvalues
    # Useful for later computing some statistics of the variance we keep
    self.eigvals = eigvals
    self.eigvecs = eigvecs

  def transform(self, Z):
      '''
      Uses a fitted PCA to transform the row vectors of Z
      Remember the eigen vectors are ordered by ascending order
      Denoting Z_trans = transform(Z),
      The first  component is Z_trans[:, -1]
      The second component is Z_trans[:, -2]
      ...
      '''
      return np.dot(Z - self.centroid, self.eigvecs[:, -self.n_components:])

Analyse de données avec pandas

Introduction

Installation

Avec uv :

~$ uv pip install pandas

Avec pip :

~$ pip install pandas

Beaucoup d’exemples par la suite viennent du guide utilisateur Pandas.

Series et DataFrame

  • une série (pd.Series) est une collection de valeurs indexées :
s = pd.Series(np.random.randn(5), index=["a", "b", "c", "d", "e"])
s.index # Index(['a', 'b', 'c', 'd', 'e'], dtype='object')
s.loc['a']
s['a']

  • une série peut être indexée, slicée, etc.. comme un tableau numpy avec iloc, et comme un dictionnaire avec [..] ou loc()

  • une DataFrame est une collection de séries de données (comme une base de données)

d = {
    "one": pd.Series([1.0, 2.0, 3.0], index=["a", "b", "c"]),
    "two": pd.Series([1.0, 2.0, 3.0, 4.0], index=["a", "b", "c", "d"]),
    "three": pd.Series([1.0, 2.0 ], index=["b", "d"])
}
df = pd.DataFrame(d)
print(df)
     one  two  three
  a  1.0  1.0    NaN
  b  2.0  2.0    1.0
  c  3.0  3.0    NaN
  d  NaN  4.0    2.0

df.loc['a',['one', 'three']] # pd.Series
  • on accède aux colonnes df.columns, à leurs types df.dtypes, à l’index df.index
  • on peut ajouter (comme un dictionnaire) des colonnes df["four"] = df["one"] + df["two"], supprimer del df["one"]

Créer une dataframe et obtenir des infos

On peut construire une DataFrame à partir de dictionnaires, tableaux numpy, … ou de fichiers :

# Dictionnaire des colonnes
d = {
    "one": pd.Series([1.0, 2.0, 3.0], index=["a", "b", "c"]),
    "two": pd.Series([1.0, 2.0, 3.0, 4.0], index=["a", "b", "c", "d"]),
    "three": pd.Series([1.0, 2.0 ], index=["b", "d"])
}
df = pd.DataFrame(d)

# Liste des lignes
df = pd.DataFrame([{"one": 1, "two": 2}, {"one": 5, "two": 10, "three": 20}])

# Fichier CSV
df = pd.read_csv("fichier.csv", delimiter=";")
  • on obtient des infos avec df.info(), df.describe(), df.head()
  • statistiques descriptives (mean, std, count) df.describe(), (unique, top, freq) df.describe(include='category')

Summarize data cheatsheets pandas

Summarize data cheatsheets pandas

Vérifier et corriger les types

  • Les types des colonnes peuvent être le type générique “object”.
  • si des données sont des temps (datetime), des données catégorielles categories, des données numériques, il faut fixer les types
def read_data(filepath: str):
    df = pd.read_csv(filepath, delimiter=";")
    return df

def fix_datatypes(df):
    cat_columns = ['code_station', 'libelle_station', ...]
    for c in cat_columns:
        df[c] = df[c].astype('category')

    df["date_observation"] = pd.to_datetime(df["date_observation"])

df = read_data("ecoulements.csv")
fix_datatypes(df)

Changing Type cheatsheets pandas

Changing Type cheatsheets pandas

Important fixer les types des séries permet de profiter de toutes les fonctionnalités associées (e.g. catégories, temps)

Calculer des statistiques descriptives

Sur une dataframe, on peut :

  • calculer des moyennes, sommes, médianes : df["Age"].median()
  • agréger avec une liste de fonctions prédéfinies (min, max, mean, …) ou arbitraires df.agg({"Age": ["min", "max", "median", "skew"]})

Les statistiques peuvent être calculées sur des sous-groupes formés par groupby:

titanic = pd.read_csv("data/titanic.csv")



# On peut regrouper les données par catégories et calculer
# des statistiques sur les sous-groupes
titanic = pd.read_csv("titanic.csv") 
grouped = titanic[["Sex", "Pclass", "Age", "Fare"]].groupby(["Sex", "Pclass"])
print(grouped.size())
print(grouped.mean())
   PassengerId  Survived  Pclass  ...     Fare Cabin  Embarked
0            1         0       3  ...   7.2500   NaN         S
1            2         1       1  ...  71.2833   C85         C
2            3         1       3  ...   7.9250   NaN         S

Sex     Pclass
female  1          94
        2          76
        3         144
male    1         122
        2         108
        3         347
dtype: int64
                     Age        Fare
Sex    Pclass                       
female 1       34.611765  106.125798
       2       28.722973   21.970121
       3       21.750000   16.118810
male   1       41.281386   67.226127
       2       30.740707   19.741782
       3       26.507589   12.661633

Voir https://pandas.pydata.org/docs/dev/getting_started/intro_tutorials/06_calculate_statistics.html#min-tut-06-stats

Pivot

Partant d’une représentation empilée (stacked), on peut réarranger les données avec la méthode pivot ou pivot_table (permet d’agréger) :

  • index : la ou les colonnes qui servent d’index
  • columns : les valeurs que ces colonnes prennent deviennent les colonnes
  • values : les valeurs à l’intersection des valeurs d’index et des valeurs de colonnes
df = pd.DataFrame(
    {
        "A": ["one", "one", "two", "three"] * 6,
        "B": ["bidule", "machin", "truc"] * 8,
        "C": ["foo", "foo", "foo", "bar", "bar", "bar"] * 4,
        "D": np.random.randn(24),
        "E": np.random.randn(24),
        "F": [datetime.datetime(2013, i, 1) for i in range(1, 13)]
        + [datetime.datetime(2013, i, 15) for i in range(1, 13)],
    }
)
print(df)

pivoted = pd.pivot_table(df, values="D", index=["A", "B"], columns=["C"])
print(pivoted)

print(pivoted.loc[("one", "bidule"), "bar"])
        A       B    C         D         E          F
0     one  bidule  foo  0.029577  0.050984 2013-01-01
1     one  machin  foo -0.442099 -0.106008 2013-02-01
2     two    truc  foo  1.953053  1.265677 2013-03-01
3   three  bidule  bar -1.299982  0.762093 2013-04-01
4     one  machin  bar  0.652348 -0.323386 2013-05-01
5     one    truc  bar  1.433064 -1.818466 2013-06-01
6     two  bidule  foo  2.291547 -0.087507 2013-07-01
7   three  machin  foo -1.203084 -0.089323 2013-08-01
8     one    truc  foo  1.022026 -1.088463 2013-09-01
9     one  bidule  bar -0.433758  2.892209 2013-10-01
...

C                  bar       foo
A     B                         
one   bidule  0.243642 -0.317265
      machin -0.183342 -0.318656
      truc    0.942341  1.991506
three bidule -0.641189       NaN
      machin       NaN -1.362425
      truc   -1.088678       NaN
two   bidule       NaN  1.272628
      machin -0.686480       NaN
      truc         NaN  1.024224

0.24364165912866229

pivot retourne une erreur en cas de doublons (moins flexible). pivot_table agrège les doublons (e.g. défaut : aggfunc='mean').

Joindre des tables

On peut joindre plusieurs dataframes par des clés, e.g. :

  • une table définit des campagnes de mesures avec leurs dates, l’opérateur, etc…
  • une table contient des observations, associées à un identifiant de campagne de mesures

Ces tableaux peuvent être joints, par exemple pour lister les observations réalisées par un opérateur.

Illustration de pd.merge dans les cheatsheets pandas

Illustration de pd.merge dans les cheatsheets pandas

Tracer des données

Pandas est interfacée avec matplotlib pour le tracé d’histogrammes (hist), nuages de points (scatter), séries (plot, même avec le temps !)

Les fonctions de tracé conduisent à des tracés indépendants pour des données groupées groupby.

Illustration des fonctions de tracés dans les cheatsheets pandas

Illustration des fonctions de tracés dans les cheatsheets pandas

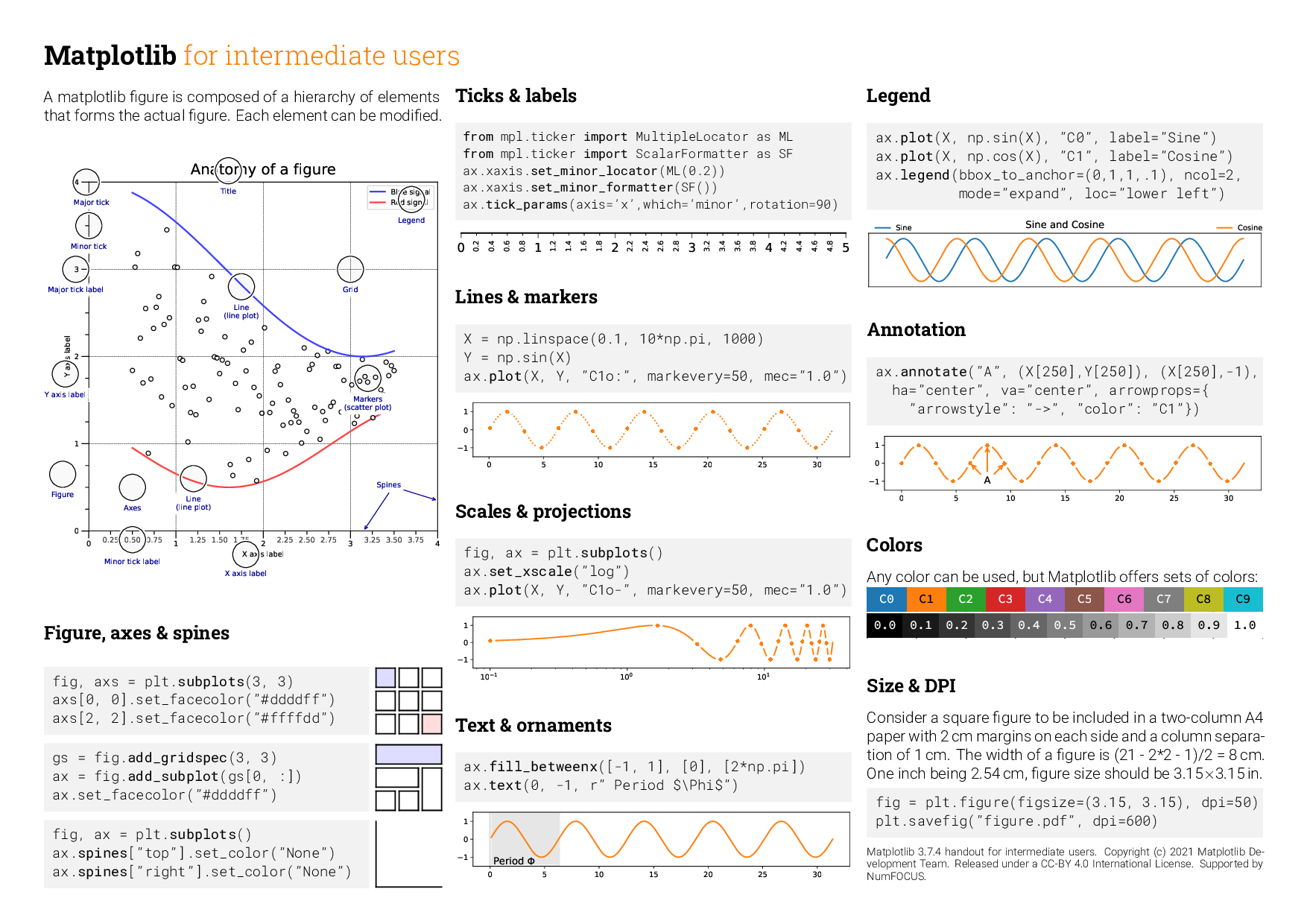
Tracés avec Matplotlib

Introduction

Matplotlib : Numerical Python

  • Librairie python pour le tracé
  • offre une multitude de fonctions de tracés plans (line plot, image, histograms), 3D statiques ou animés

Mission statement

Adapting the requirements laid out by John Hunter Matplotlib should:

  • Support users of the Scientific Python ecosystem;
  • Facilitate interactive data exploration;
  • Produce high-quality raster and vector format outputs suitable for publication;
  • Provide a simple graphical user interface and support embedding in applications;
  • Be understandable and extensible by people familiar with data processing in Python;
  • Make common plots easy, and novel or complex visualizations possible.
import matplotlib
import matplotlib.pyplot as plt

Matplotlib for beginners

Handout for beginners de la documentation de matplotlib disponible sur https://matplotlib.org/cheatsheets/_images/handout-beginner.png

Handout for beginners de la documentation de matplotlib disponible sur https://matplotlib.org/cheatsheets/_images/handout-beginner.png

Matplotlib for intermediate users

Handout for intermediates de la documentation de matplotlib disponible sur https://matplotlib.org/cheatsheets/_images/handout-intermediate.png

Handout for intermediates de la documentation de matplotlib disponible sur https://matplotlib.org/cheatsheets/_images/handout-intermediate.png

Les cheatsheats (1/2)

Cheatsheet 1 : disponible en ligne : https://matplotlib.org/cheatsheets/_images/cheatsheets-1.png

Cheatsheet 1 : disponible en ligne : https://matplotlib.org/cheatsheets/_images/cheatsheets-1.png

Les cheatsheats (2/2)

Cheatsheet 2 : disponible en ligne : https://matplotlib.org/cheatsheets/_images/cheatsheets-2.png

Cheatsheet 2 : disponible en ligne : https://matplotlib.org/cheatsheets/_images/cheatsheets-2.png

Apprentissage automatique avec scikit-learn

Introduction à l’apprentissage supervisé

Quelques concepts clés pour fixer les idées :

  • On suppose disposer de données \(x_i\) qui peuvent être étiquetées \(y_i\)

  • Apprentissage supervisé :

    Etant donnés des paires \((x_i, y_i) \sim P_{X, Y}\), apprendre une fonction \(f_\theta\) (un prédicteur) qui minimise le risque réel :

\[ R_r(f) = \int_{X \ times Y} \mathcal{L}(y, f_\theta(x)) p_{X, Y}(x,y) dx dy \]

  • Etant données un échantillonnage \((x_i, y_i), i \in [|0, N-1|]\), on peut calculer le risque empirique :

\[ R_e(f) = \sum_{i=0}^{N-1} \mathcal{L}(y_i, f_\theta(x_i)) \]

Question : comment prédire l’étiquette \(y\) associée à des \(x\) étant données des paires d’échantillons \((x_i, y_i)\)

Attention nous ne pourrons pas introduire tout les concepts liés au machine learning

Qu’apporte scikit-learn ? Une vue d’ensemble

Scikit-learn est une librairie python qui offre:

Le tout étant pipelinable et disposant d’une interface commune.

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

# Chargement des données
iris = load_iris()
X, y = iris.data, iris.target

# Construction d'un pli d'entrainement et un pli de test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# Construction du prédicteur et entrainement
clf = make_pipeline(StandardScaler(), KNeighborsClassifier(3))
clf.fit(X_train, y_train)

# Evaluation du risque sur un pli de test
score = clf.score(X_test, y_test)

# Inférence sur le pli de test
y_test_pred = clf.transform(X_test)

Scikit-learn

Scikit-learn

Exemples de régression et classification

Voir Feature_selection_embedded.html

Ressources

Benureau, Fabien C. Y., and Nicolas P. Rougier. 2018. “Re-Run, Repeat, Reproduce, Reuse, Replicate: Transforming Code into Scientific Contributions.” Frontiers in Neuroinformatics Volume 11 - 2017. https://doi.org/10.3389/fninf.2017.00069.
Hayes, Brian. 2000. “Computing Science: The World in a Spin.” American Scientist 88 (5): 384–88. http://www.jstor.org/stable/27858079.
Sethna, James P. 2006. “Statistical Mechanics: Entropy, Order Parameters, and Complexity, 2nd Edition, Chap 8.” In Oxford Master Series in Physic. Univ. Press.